Применение численных методов для решения математических задач. курсовая работа (т). математика. 2012-12-06

Как управлять компьютером без мышки

Что делать, если мышь на компьютере зависла и не позволяет переключаться между окнами и перезагружать машину? Давайте научимся управлять компьютером без мыши, освоив простые шаги, описанные в нашей статье.

С ноутбуками проще — с ними можно работать с помощью тачпада. Но бывают ситуации, когда ломаются оба манипулятора. В этом случае помогут наши советы по управлению компьютером без мышки.

Как работает клавиатура компьютера без мышки (режим эмуляции)

Используйте клавиатуру для управления курсором на экране. Для этого используйте цифровые клавиши, которые вынесены в отдельный блок справа.

Удерживайте клавиши Alt и Shift влево и включите цифровую клавиатуру с помощью Num Lock. ПК подаст звуковой сигнал и откроет диалоговое окно.
Несколько раз нажав клавишу Tab, выберите строку, ведущую к Центру специальных возможностей, и нажмите клавишу пробела.
В окне с помощью той же клавиши Tab перейдите к указателям, управляющим скоростью движения курсора. Стрелки клавиатуры помогают установить максимальные значения.
Выделите кнопку Применить и нажмите Enter.
Закройте окно с помощью Alt + F4.

Мы снова открываем диалоговое окно, как описано в шаге 1, выбираем кнопку Tab «Да» и нажимаем Enter.

Все числа, кроме 0 и 5, указывают направление движения на экране. «Пятерка» работает как ЛКМ (двойной щелчок заменяет двойной щелчок, «+» используется с той же целью), «-» — ПКМ. «0» удерживает выбранную кнопку весла, «.» — пойдем. Нажатие NumLock отменяет режим эмуляции, а повторное нажатие восстанавливает его. Эта функция полностью отключается, если открыть диалоговое окно (как в шаге 1) и нажать «Нет».

Выходим на рабочий стол и панель задач

Курсор, управляемый клавиатурой, движется не очень быстро. Ситуацию можно упростить, используя комбинацию win + d. При этом открываются папки и запускаются ярлыки, размещенные на рабочем столе. По нажатию win+d видим выделение на одной из иконок. Перемещаемся между иконками с помощью стрелочек, а с помощью Enter открываем папки и запускаем ярлыки программ.

Если открытое окно программы не позволяет перейти на рабочий стол, попробуйте использовать комбинацию win+m.

Чтобы получить доступ к панели задач, перейдите на рабочий стол и нажмите Tab. Также переключаемся между элементами системы с помощью Tab, между открытыми пользователем приложениями — стрелками, запускаем программы — Enter, а раскрывающиеся списки открываем пробелом.

Управляем окнами

Для работы в активной папке или программе используйте клавиши Tab, Alt, стрелки. Закройте все окна по одному с помощью Alt+F4.

Вызываем диспетчер задач

Чтобы позвонить, нажмите ctrl+shift+esc. Затем используем ключи, которые были описаны в предыдущем разделе. Завершаем активный процесс удаления и подтверждаем действие Enter.

Перезагружаем компьютер и блокируем экран

Перезагрузите компьютер, нажав Alt+F4 или ctrl+alt+delete. Или зайдите в «Пуск» и выберите нужное действие.

Экран блокировки вызывается комбинацией win+L. Но чтобы эта функция работала, мы сначала устанавливаем пароль на компьютер.

Как видите, с помощью клавиатуры можно выполнять различные действия без мыши. Далее мы предоставим список сочетаний клавиш, которые позволят вам освоить другие полезные функции.

Советы по оптимальному использованию кнопки СКМ

Кнопка СКМ, или средняя кнопка мыши, может быть полезным инструментом во многих ситуациях. Вот несколько советов, которые помогут вам оптимально использовать эту кнопку:

1.	Открывать ссылки в новых вкладках:	Если вы хотите открыть ссылку в новой вкладке, просто нажмите на нее средней кнопкой мыши. Это позволит вам быстро просмотреть содержимое ссылки, не покидая текущую страницу.
2.	Прокручивать веб-страницы:	СКМ также может использоваться для прокрутки веб-страниц. Просто нажмите и удерживайте среднюю кнопку и двигайте мышь вверх или вниз, чтобы прокручивать страницу в соответствующем направлении.
3.	Открывать закладки в новых вкладках:	Если у вас много закладок, а вы хотите открыть одну из них в новой вкладке, нажмите на закладку средней кнопкой мыши. Таким образом, вы сможете быстро открыть несколько закладок одновременно.
4.	Перетаскивать и открывать ссылки:	СКМ также позволяет перетаскивать ссылки. Просто нажмите и удерживайте среднюю кнопку мыши над ссылкой, затем переместите мышь в желаемое место и отпустите кнопку, чтобы открыть ссылку в новой вкладке или окне.
5.	Закрывать вкладки:	Если у вас открыто много вкладок и вы хотите быстро закрыть одну из них, просто нажмите на вкладку средней кнопкой мыши. Это сделает процесс закрытия вкладки гораздо более эффективным и удобным.

С помощью этих советов вы сможете максимально использовать кнопку СКМ на клавиатуре и сделать свой опыт работы с компьютером еще более удобным и эффективным.

История[править | править код]

Вычислительная математика возникла довольно давно. Ещё в Древней Месопотамии были разработаны методы получения квадратного корня. В эпоху научной революции вычислительная математика развивалась быстрыми темпами из практических применений параллельно с математическим анализом. Помимо этого, подобные вычисления широко применялись в небесной механике для предсказания траектории движения небесных тел. Это привело к появлению таких важнейших составляющих физики, как теория о гелиоцентрической системе устройства мира, законы Кеплера и законы Ньютона. XVII и XVIII век стали временем разработки значительного количества численных методов и алгоритмов.

Применение большого количества инженерных вычислений в XIX и XX веках потребовало создания соответствующих приборов. Одним из таких приборов стала логарифмическая линейка, также появились таблицы значений функций с точностью до 16 знаков после запятой, помогавшие проводить вычисления. Также существовали механические устройства для выполнения математических операций, называвшиеся арифмометрами. В первой половине XX века для решения дифференциальных уравнений стали активно использоваться аналоговые ЭВМ.

Изобретение компьютера в середине XX века означало создание универсального инструмента для математических вычислений. Совместно с мейнфреймами в распоряжении инженеров и учёных для выполнения ручных операций были только калькуляторы, которые активно использовались вплоть до начала массового производства персональных компьютеров.

Элементы теории информации в кибернетике и вычислительной математике

Вычислительная математика и кибернетика, как и многие другие области науки, тесно связаны с теорией информации. Элементы теории информации играют важную роль в разных аспектах исследований этих наук.

Теория информации изучает методы передачи, обработки и хранения информации. В кибернетике и вычислительной математике, знания и методы из теории информации используются для оптимизации коммуникационных процессов, а также для разработки и улучшения алгоритмов обработки данных.

Одной из ключевых теорем теории информации является теорема Шеннона, которая устанавливает, что существует верхний предел на скорость передачи информации в канале связи с конечной пропускной способностью. В вычислительной математике и кибернетике эта теорема используется для оптимизации протоколов связи и повышения эффективности обмена информацией между различными компонентами системы.

Также важным элементом теории информации является понятие энтропии, которая описывает количество информации в системе. В кибернетике и вычислительной математике, знание энтропии используется для оценки эффективности сжатия данных, а также для разработки алгоритмов сжатия данных.

Теория информации также содержит понятие случайности, которое имеет ценность для криптографии и разработки алгоритмов шифрования. Например, в криптографии используется случайное число для создания ключей и обеспечения безопасности информации.

Применение кнопки СКМ в программировании и графических редакторах

Кнопка СКМ (средняя кнопка мыши) имеет широкое применение и в программировании, и в графических редакторах. Ее функциональность может значительно упростить выполнение определенных задач.

В программировании кнопка СКМ часто используется для следующих действий:

В графических редакторах кнопка СКМ также имеет важное значение:

Панорамирование изображения. Если зажать СКМ и перемещать мышь, изображение будет плавно перемещаться, позволяя просмотреть разные части больших изображений.
Увеличение и уменьшение масштаба. Зажатие СКМ и перемещение мыши вверх или вниз позволит быстро увеличить или уменьшить масштаб изображения.
Выделение области для редактирования. Зажатие СКМ позволяет выделить определенную область изображения для последующего редактирования.

Использование кнопки СКМ в программировании и графических редакторах позволяет значительно повысить эффективность работы, сократить количество необходимых действий и упростить выполнение различных задач.

Как работает СКМ на клавиатуре?

Положение кнопки на клавиатуре лэптопа

Для чего нужна кнопка «шифт»

Кнопку «шифт» на ноутбуке пользователям приходится нажимать часто, как во время набора текста, так и для активации дополнительных функций. При этом знания владельцев ПК о возможностях клавиши ограничены, хотя некоторые полезные комбинации с ней облегчают работу и ускоряют выполнение привычных задач.

СКМ — ЗАО «Систем Кэпитал Менеджмент» управляющая компания финансово промышленной группы СКМ (Украина); СКМ РФ Союз коммунистической молодёжи Российской Федерации общероссийская общественная организация; Средняя кнопка мыши… … Википедия

Помимо упомянутого выше сочетания клавиш, на современных клавиатурах есть полноценная кнопка вызова контекстного меню. Расположена она между правыми кнопками Windows и Ctrl (см. рисунок ниже) и выглядит как список со стрелочкой, указывающей на один из пунктов.

Что такое ПКМ на компьютере | RMB

СКМ РФ — Союз коммунистической молодёжи Российской Федерации (КПРФ) молодёжная политическая организация, политически близкая к КПРФ. Союз коммунистической молодёжи Российской Федерации (независимый) независимая политическая молодежная общероссийская… … Википедия

СКМ — служба криминальной милиции Словарь: Словарь сокращений и аббревиатур армии и спецслужб. Сост. А. А. Щелоков. М.: ООО «Издательство АСТ», ЗАО «Издательский дом Гелеос», 2021. 318 с. СКМ сцепка канатная механизированная в маркировке Пример… … Словарь сокращений и аббревиатур

Смотреть что такое «СКМ» в других словарях:

Гарантия качестваНа нашем мебельном производстве каждый этап производства строго контролируется. Вся выпускаемая продукция проверяется на соответствие действующим нормативам. На всю мебель предоставляется гарантия 18 месяцев.

Joy1 — Joy32: кнопки джойстика. Для удобства определения номеров кнопок вашего джойстика был создан специальный тест-скрипт (см. ссылку в оригинале статьи)

Обратите внимание, что такие префиксы, как ^ (control) и + (shift) здесь не поддерживаются (тем не менее, команда GetKeyState может использоваться). Также обратите внимание, что нажатия клавиш джойстика всегда обращены напрямую в активное окно, поддерживающее приём таких сигналов

Linux

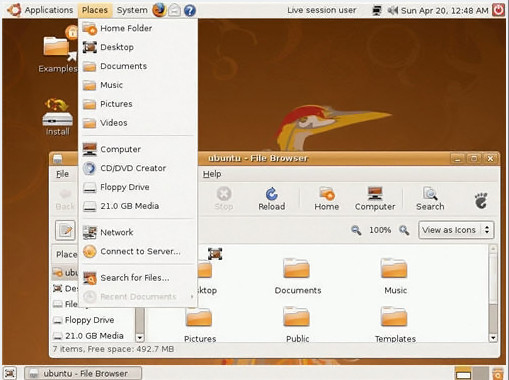
Linux — семейка операционных систем с открытым исходным кодом. Это значит, они могут модифицироваться (изменяться) и распространятся любым человеком по всему миру. Это очень отличает эту ОС от других, таких как Windows, которая может изменяться и распространяться только самим владельцем (Microsoft). Преимущества Линукса в том, что он бесплатный, и есть много различных версий на выбор. Каждая версия имеет свой внешний вид, и самые популярные из них это Ubuntu
, Mint
и Fedora
.

Linux назван в честь Линуса Торвальдса, который заложил основу в Linux в 1991 году.

По данным общей статистики StatCounter Global Stats, процент пользователей Linux составляет менее 2% рынка операционных систем, по состоянию на сентябрь 2014 года. Однако, из-за гибкости и легкости в настройках большинство серверов работают на Linux.

Apple Mac OS X

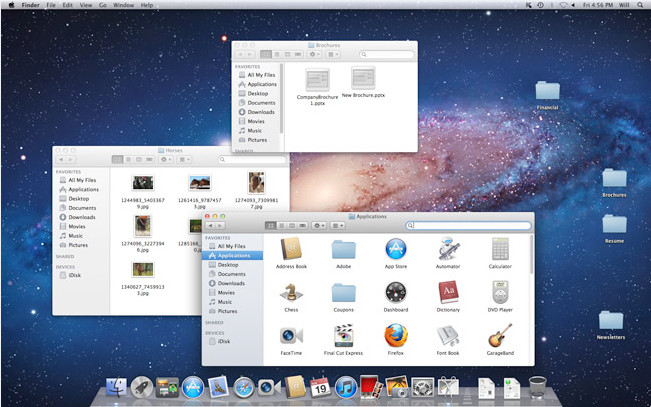
Mac OS представляет собой линейку операционных систем, созданных компанией Apple. Она поставляется предустановленной на всех новых компьютерах Macintosh или Mac. Последние версии этой операционной системы известны как OS X
. А именно Yosetime
(выпущенный в 2014 году), Mavericks
(2013), Mountine
Lion
(2012), Lion
(2011), и Show Leopard
(2009). Также есть Mac OS X Server
, который предназначен для работы на серверах.

По данным общей статистики StatCounter Global Stats, процент пользователей Mac OS X составляет 9,5% рынка операционных систем, по состоянию на сентябрь 2014 года. Это намного ниже чем процент пользователей Windows (почти 90%
). Одной из причин этого является то что компьютеры Apple очень дорогие.

Что такое «ПКМ»? Что нужно знать и понимать

Откровенно говоря, любой пользователь, не знающий, как расшифровывается это сокращение, просто приводит в состояние крайнего недоумения! Ну неужели, даже при самой примитивной попытке интерпретации данного сокращения не может прийти на ум нечто вроде «Правого клика мышью» или аналогичного «Правой кнопки мыши»?

Конечно, многие из новоявленных пользователей, впервые столкнувшихся с объектно-ориентированными системами на основе доступа к основным функциям посредством дополнительных меню, спрашивают о том, что такое «ПКМ». К сожалению, нужно сразу огорчить всех юзеров этого уровня. Не знать, что такое «ПКМ», — значит, не знать вообще ничего.

Горячие клавиши на клавиатуре

Не могу сказать. Я не тестирую и не работаю на всех компьютерах, ноутбках и моноблоках. У каждого компьютерного устройства есть инструкция, где описано как конкретно с этим устройством работать — как войти в БИОС, как вернуть компьютер к заводским настройкам и так далее. Обращайтесь всегда в первую очередь к документации.

Здравствуйте,Андрей!Прочитав отзывы Ваших подписчиков,поняла,что сайт запущен давно,а я методом тыка набрела случайно и сразу же подписалась.В отличие от множества сайтов,просмотренных в ин-те,которые грешат многословием и обилием спец.терминов,Ваши пояснения конкретны и функциональны.Спасибо за уроки.Компьютер для меня и универсальный справочник,и библиотека,и кинотеатр.В моем очень пенсионном возрасте простые и понятные объяснения очень вожнны.Спасибо,буду ждать продолжения.

Как использовать Скм на клавиатуре

СКМ (сокращение от «средняя клавиша мыши») — это средняя кнопка на мышке, которая обычно представлена в виде колесика.

СКМ имеет несколько полезных функций:

Прокрутка страницы: Если вы нажмете на СКМ и начнете двигать колесико вверх или вниз, то сможете быстро прокручивать содержимое на странице. Это особенно полезно, когда нужно быстро промотать длинный текст или просмотреть большое количество изображений.
Открытие ссылок в новой вкладке: Если вы средней кнопкой мыши нажмете на ссылку, то она откроется в новой вкладке вашего браузера без перехода со страницы, на которой сейчас находитесь. Это может быть удобно, когда вы хотите открыть несколько ссылок и вернуться к ним позже, не теряя место, где вы были до этого.
Закрытие вкладок: Если вы средней кнопкой мыши нажмете на открытую вкладку в вашем браузере, то она закроется мгновенно. Это удобно, когда у вас открыто много вкладок и вы хотите быстро избавиться от одной из них.

Сочетания клавиш СКМ на клавиатуре
Сочетание клавиш
Описание

Ctrl + СКМ

Открыть ссылку в новой вкладке

СКМ на открытой вкладке
Закрыть текущую вкладку

Использование СКМ на клавиатуре может значительно повысить вашу эффективность при работе с компьютером. Попробуйте использовать эти функции и вы обнаружите, что ваша работа станет более удобной и быстрой.

Особенности представления чисел в компьютере[править | править код]

Основное отличие вычислительной математики заключается в том, что при решении вычислительных задач человек оперирует машинными числами, которые являются дискретной проекцией вещественных чисел на конкретную архитектуру компьютера. Так, например, если взять машинное число длиной в 8 байт (64 бита), то в нём можно запомнить только 264 разных чисел, поэтому важную роль в вычислительной математике играют оценки точности алгоритмов и их устойчивость к представлениям машинных чисел в компьютере. Именно поэтому, например, для решения линейной системы алгебраических уравнений очень редко используется вычисление обратной матрицы, так как этот метод может привести к ошибочному решению в случае с сингулярной матрицей, а очень распространённый в линейной алгебре метод, основанный на вычислении определителя матрицы и её дополнения, требует гораздо больше арифметических операций, чем любой устойчивый метод решения линейной системы уравнений.

Литература[править | править код]

Вычислительная математика / А. Н. Тихонов // : / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Марчук Г. И. Методы вычислительной математики. — Новосибирск: Наука, 1973.
Бабенко К. И. Основы численного анализа. — М.: Наука, 1986.
Бахвалов Н. С. Численные методы. 3-е изд. — М., 2003.
Воеводин В. В. Математические основы параллельных вычислений. — М.: Изд-во МГУ, 1991. — 345 с.
Воеводин В. В., Воеводин Вл. В. Параллельные вычисления. — СПб.: БХВ-Петербург, 2002. — 608 с.
Демидович Б. П., Марон И. А. Основы вычислительной математики. — 2-е изд. — М.: Государственное издательство физико-математической литературы, 1963.
Дьяченко В. Ф. Основные понятия вычислительной математики. — М.: Наука, 1972.
Вычислительные методы для анализа моделей сложных динамических систем : Учеб. пособие для студентов вузов по напр. «Прикладные математика и физика» / А. И. Лобанов, И. Б. Петров; М-во образования Рос. Федерации. МФТИ (гос. ун-т). — М. : МФТИ, 2000. — 21 см.
- Ч. 1. — 2000. — 168 с. : ил., табл.; ISBN 5-7417-0149-3
- Ч. 2. — 2002. — 154 с. : ил.; ISBN 5-7417-0199-X
Вычислительная математика : курс лекций / А. И. Лобанов, И. Б. Петров. — Москва : Физматкнига, 2021. — 475 с. : ил.; 22 см. — (Физтеховские курсы).; ISBN 978-5-89155-341-5 : 300 экз.
Канторович Л. В., Крылов В. И. Приближённые методы высшего анализа. — М.—Л.: ГИИТЛ, 1949.

Примеры работы СКМ на компьютере

Системы контроля версий (СКМ) предлагают широкий спектр функций и возможностей для управления версиями файлов и совместной работы над проектами. Вот несколько примеров работы СКМ на компьютере:

Отслеживание изменений файлов: СКМ позволяет отслеживать все изменения, сделанные в файлах проекта. Вы можете видеть, какой файл был изменен, кем и когда это было сделано. Это позволяет вам контролировать историю изменений и восстанавливать предыдущие версии файлов при необходимости.
Совместная работа над проектами: СКМ предоставляет средства для совместной работы над проектом. Несколько разработчиков могут работать над одним и тем же файлом или проектом и легко сливать свои изменения. Каждый разработчик может вносить свои изменения в свою «ветку» проекта, а затем объединять их с общим репозиторием. Это позволяет избежать конфликтов и упрощает работу в команде.
Восстановление предыдущих версий: Если вы случайно удалили или испортили файл, вы можете легко восстановить предыдущую рабочую версию из СКМ. СКМ сохраняет все предыдущие версии измененных файлов, поэтому вы можете откатиться к любому состоянию проекта, которое вам нужно.
Организация и управление проектами: СКМ позволяет создавать отдельные репозитории для каждого проекта или группы файлов. Вы можете организовать свои проекты, ветки и команды разработчиков, используя типичные операции, такие как создание, удаление и объединение веток, а также слияние и разрешение конфликтов.
Отслеживание ошибок и исправления: СКМ часто используется для управления баг-трекерами и отслеживания ошибок в рамках проектов. Вы можете привязывать изменения в коде к определенным задачам или ошибкам, отслеживать выполнение и автоматически ассоциировать исправления с соответствующими задачами.

Приведенные примеры являются лишь некоторыми из множества возможностей, которые СКМ предоставляет

Каждая система контроля версий может иметь свои особенности и специфические функции, поэтому важно смотреть на конкретные возможности каждой системы перед ее использованием

Важность использования Скм на клавиатуре

Скм на клавиатуре (сочетание клавиш на клавиатуре) является одним из важных инструментов для выполнения различных команд и функций на компьютере. Он позволяет пользователю получить доступ к разнообразным функциям, упрощает работу и повышает эффективность использования компьютера.

Преимущества использования Скм на клавиатуре:

Сокращение времени работы: с помощью сочетаний клавиш можно выполнять множество операций быстрее, чем при использовании мыши. Это особенно полезно для людей, работающих с текстами, графикой или программированием.
Улучшение эргономики: использование Скм позволяет снизить нагрузку на запястья, руки и плечи, что помогает предотвращать развитие травм репетитивного напряжения.
Повышение производительности: благодаря использованию комбинаций клавиш можно быстро переключаться между приложениями, открывать новые вкладки в веб-браузере, копировать и вставлять текст и многое другое.
Удобство использования: Скм позволяет быстро доступаться к часто используемым функциям без необходимости поиска соответствующих команд в меню программы.

Наиболее часто используемые комбинации клавиш:

Сочетание клавиш	Описание
Ctrl+C	Копирование выделенного текста или объекта
Ctrl+V	Вставка скопированного текста или объекта
Ctrl+Z	Отмена последнего действия
Ctrl+X	Вырезание выделенного текста или объекта
Ctrl+S	Сохранение текущего документа или файла
Ctrl+P	Печать текущего документа

Использование Скм на клавиатуре позволяет повысить эффективность работы, улучшить эргономику и удобство использования компьютера. Рекомендуется изучить и запомнить наиболее часто используемые сочетания клавиш для оптимального использования всех возможностей компьютера.

Расположение и назначение кнопки СКМ на клавиатуре

Назначение кнопки СКМ состоит в осуществлении дополнительных функций при нажатии не на саму кнопку, а на колесо мыши, которое может прокручиваться вверх и вниз. Кнопка СКМ позволяет пользователю выполнять различные действия, в зависимости от контекста использования.

Одно из самых распространенных использований кнопки СКМ — прокрутка страницы веб-браузера или текста в документе. Чтобы выполнить прокрутку, необходимо нажать кнопку СКМ и перемещать колесо мыши вверх или вниз. Прокрутка выполняется плавно и позволяет легко и быстро перемещаться по содержимому страницы или документа.

Также кнопка СКМ может выполнять другие функции в различных приложениях. Например, в графических редакторах кнопка СКМ может использоваться для перемещения изображения на экране или изменения его масштаба. В некоторых программах и играх кнопка СКМ может иметь свои собственные дополнительные функции и назначения, которые зависят от конкретного приложения.

Важно отметить, что функциональность кнопки СКМ может варьироваться в зависимости от операционной системы, настройки системы и используемого программного обеспечения. Чтобы узнать все возможности кнопки СКМ в конкретной ситуации, рекомендуется обратиться к соответствующей документации или помощи программы, которую вы используете

Развитие метода Эйлера в работах Коши

Трудно переоценить тот вклад, который внес 0Коши (1789 -1857) в развитие численных методов решения дифференциальных уравнений, Коши глубоко проанализировал подходы к приближенному решению дифференциальных уравнений и нашел пробелы в решении этой проблемы его предшественниками. Он заметил, что интегрирование дифференциальных уравнений при помощи степенных рядов не дает никакого средства для выяснения- вопроса — являются ли полученные ряды сходящимися, а их суммы — функциями, удовлет -ворявдими данным уравнениям, Коши обосновал метод степенных рядов. Вместе с тем он глу -боко заинтересовался методом Эйлера численного решения дифференциальных уравнений 1-го порядка при начальном условии Критически осмыслив метод, Коши развил его, доказав, в предположении ограниченности и непрерывности fOcuJm. в области IX-X0I Qju-U0l&Q существование единствен ного решения задачи (2.8), (2.9) в интервале/Jf-J / / , где / — наименьшее из чисел й и -тт» t a M=m&x/f(X,yJ/. Один из способов доказательства этой теоремы представляет собой теоретическое обоснование метода Эйлера. Он состоит в том, что дифференциальное уравнение рассматривается как предел уравнений в конечных разностях. Уравнение (2.8) заменяется приближенным равенством Интервал ( Х0 у X )» где Х= Хп , Копій делит на частичные интервалы (X0fX,)f (X,,Jb), —/ ,, . Из уравнения — -=f(X0M0)(Xf-Xo) однозначно определяется и и устанавли вается неравенство Чтобы выполнялось условие IU-иб[ и , нужно выбрать /Х-Х / f й этом условии величина j (Хп У,) при нимает определенное значение и уравнение однозначно определяет иг Так как то для выполнения условия 1иг-ио/к:и нужно выбрать /Х2-Х0/ — г Продолжая аналогичные рассуждения, Коши поду лучает уравнение однозначно определяющее Уд-/ t и для выполнения неравенства

Таким образом, приближенное значение искомого решения в точке Коши записывает, как и Эйлер, Но Коши доказал сходимость при /?- -оо приближенного решения у к предельной уякщи у(Х) » а также доказал, что у(Х) является решением поставленной задачи и притом единственным. После обоснования Коши метода ломаных Эйлера задача нахождения решения дифференциальных уравнений с начальными условиями стала называться задачей Коши. Методы доказательства теоремы существования и единственности решения задачи (2.8),(2.9) Коши изложил в своих лекциях по интегральному исчислению, которые он читал в Парижской политехнической школе в 1820-30 годах. Второй том лекций, в котором рассматривались эти вопросы, не был опубликован. 0 результатах, содержащихся в нем, мы можем судить по лекциям, зали санным его учеником %аньо [219, т.2, cTp.395-4I0J , Коши впервые исследовал погрешность метода Эйлера и полу -чил рекуррентную оценку погрешности на /7 -ом шаге, а также независимую оценку погрешности . Пусть X и у изменяются соответственно в промежутках ная, удовлетворяющая условию fj (Х,у)/ Д для ука занных X U Кши пшяимает , что в рассматриваемой облас ттт иомоиоитт тто-пар.тиazrv тя.тттгі7Тоатптг а псітлпт аиг гттпа / V I «/ /У I t лы Ах 6 Затем строится ломаная с началом в точке П= Ц и вершинами в точках, полученных по формуле Quti = = ynt f(XntUn) АХ . Если Ц(Х) — ордината конца этой ломаной, тогда разность lu(X)- U(X)I , согласно Коши, будет меньше Из этой оценки видно, что при 0 0 приближенное решение сходится к точному.

Доказательство этой оценки имелось,видимо , в упомянутых лекциях по интегральному исчислению. Формулы Коши для оценки погрешности не получили практичес -кого применения, поскольку увеличение погрешности по экспопен -циальному закоігу значительно превышает фактическую погрешность. Коши разработал усовершенствование метода ломаных Эйлера, которое получило применение на практике. По этому методу вначале находится вспомогательное значение искомого решения Ц{л) ПРИ X = Xrj ДДЯ уравнения (2.8) по формуле Эйлера: где fj — длины частичных интервалов. Затем приближения искомого решения U (х) находятся по формуле : Таким образом Коши впервые использует зависимость правой части уравнения У — -f (Хи) от самой неизвестной функции ц(х) и пользуясь этим, получает метод Эйлера с итерациями. Коши не привел формулу в общем виде, но подробно описал алгоритм на примере решения дифференциального уравнения при начальном условии u(0)=0 в 1890 г. Строгая обработка Коши методов Эйлера, с одной стороны , способствовала развитию нового направления анализа — анаяити -ческой теории дифференциальных уравнений. С другой стороны -открывала возможности для применения и развития численных ме -тодов решения дифференциальных уравнений, роль которых возросла после доказательства Диувшілем в 1841 г неразрешимости общего уравнения Риккати в элементарных функциях.

S-PLUS

S-PLUS — продукт компании Insightful Corporation (http://www.insightful.com/),
ранее известной как подразделение MathSoft, а теперь являющейся одним из мировых
лидеров в области статистического анализа данных, визуализации и прогнозирования.
S-PLUS представляет собой интерактивную компьютерную среду, обеспечивающую полнофункциональный
графический анализ данных и включающую оригинальный объектно-ориентированный
язык. Гибкая система S-PLUS может использоваться для исследовательского анализа
данных, статистического анализа и математических вычислений, а также для удобного
графического представления анализируемых данных. К основным достоинствам S-PLUS
относятся непревзойденная функциональность, возможность интерактивного визуального
анализа данных, интуитивно понятные интерфейс пользователя и методы подготовки
анализируемых данных, простота использования самых современных статистических
методов, мощные вычислительные возможности, расширяемый набор статистических
методов, гибкий интерфейс пользователя. Цена — 2865 долл.

КомпьютерПресс 12″2001

Задачи для самостоятельного решения[править]

Читателю предлагается добраться до компьютера и компилятора какого-нибудь языка программирования (Си или Pascal) и провести несколько незатейливых численных экспериментов.

Задача 1 (частичная сумма гармонического ряда).править

Напишите программу, которая суммирует первые миллион слагаемых гармонического ряда сначала с первого по последний элемент, а потом наоборот — с последнего по первый:
A=11+12+13+…+1106=1106+…13+12+11{\displaystyle A={1 \over 1}+{1 \over 2}+{1 \over 3}+\ldots +{1 \over {10^{6}}}={1 \over {10^{6}}}+\ldots {1 \over 3}+{1 \over 2}+{1 \over 1}\,\!}.
Убедитесь, что ассоциативный закон «(a+b)+c=a+(b+c){\displaystyle (a+b)+c=a+(b+c)\,\!}» при вычислении на компьютере с конечной точностью не выполняется, что может привести к довольно сильному расхождению между результатом вычислений и реальным значением выражения.

Задача 2 («страшный» предел).править

Найдите с помощью компьютера значение выражения
sin⁡(tan⁡(x))−tan⁡(sin⁡(x))arcsin⁡(arctan⁡(x))−arctan⁡(arcsin⁡(x)){\displaystyle {\frac {\sin(\tan(x))-\tan(\sin(x))}{\arcsin(\arctan(x))-\arctan(\arcsin(x))}}\,\!}

при x, равном 1, 1/2, 1/4, 1/8, 1/10, 1/100, … (x измеряется в радианах). Как вы думаете, к чему это выражение на самом деле стремится по мере того, как x стремится к 0? дайте решение пожалуйста.

Задача 3 («башня» из степеней).править

Рассмотрим функцию f(x)=xxx⋅⋅⋅{\displaystyle f(x)=x^{x^{x^{\cdot ^{\cdot ^{\cdot }}}}}\,\!}. Эта функция представляет собой бесконечную башню степеней. При некоторых x{\displaystyle x} такая бесконечная конструкция имеет смысл. Видно, что f(x)=xf(x){\displaystyle f(x)=x^{f(x)}\,\!}. Это значит, что при f(x)=a{\displaystyle f(x)=a\,\!}
имеем a=xa{\displaystyle a=x^{a}\,\!}
и x=a1a{\displaystyle x=a^{1/a}\,\!}
. Из этого можно ошибочно вывести, что при x=313=33{\displaystyle x=3^{1/3}={\sqrt{3}}\,\!}
имеем f(x)=3{\displaystyle f(x)=3\,\!}
. Это не так. Убедитесь в этом сами. Мы предлагаем вам изучить функцию f(x){\displaystyle f(x)\,\!}
, приблизив её «башней» степеней конечной высоты. А именно, рассмотрите и запрограммируйте рекурсивную функцию Fn(x)=xFn−1(x){\displaystyle F_{n}(x)=x^{F_{n-1}(x)}\,\!}
, F1(x)=x{\displaystyle F_{1}(x)=x\,\!}
. Напишите программу (или используйте GnuPlot, Mathematica, Maple или другие подобные инструменты), которая рисует график четырёх функций F1000(x){\displaystyle F_{1000}(x)\,\!},
F1001(x){\displaystyle F_{1001}(x)\,\!}, F1002(x){\displaystyle F_{1002}(x)\,\!},
F1003(x){\displaystyle F_{1003}(x)\,\!} на интервале (0;3). Из вида этих графиков сделайте выводы. При каких x{\displaystyle x} определена функция f(x){\displaystyle f(x)\,\!}, то есть при каких x{\displaystyle x} значения Fn(x){\displaystyle F_{n}(x)\,\!} при увеличении n{\displaystyle n} становятся все ближе и ближе друг к другу и к некоторому фиксированному числу?
Когда числа из последовательности a1,a2,…,an,…{\displaystyle a_{1},\;a_{2},\;\;\ldots ,\;a_{n},\;\ldots \,\!}
приближаются к некоторому числу A{\displaystyle A}, то говорят, что последовательность
ai{\displaystyle a_{i}\,\!}имеет предел A{\displaystyle A} и пишут an→A{\displaystyle a_{n}\to A\,\!}
при n→∞{\displaystyle n\to \infty \,\!}.

Уточним это понятие: какое бы маленькое положительное число ε{\displaystyle \varepsilon \,\!}
мы ни выбрали, всегда найдется такой элемент последовательности aM{\displaystyle a_{M}\,\!},
что он сам и все элементы последовательности после него оказываются удалены от числа A не более чем на ε{\displaystyle \varepsilon \,\!}

|aM−A|<ε,|aM+1−A|<ε,|aM+2−A|<ε,|aM+3−A|<ε,…{\displaystyle |a_{M}-A|<\varepsilon ,\quad |a_{M+1}-A|<\varepsilon ,\quad |a_{M+2}-A|<\varepsilon ,\quad |a_{M+3}-A|<\varepsilon ,\quad \ldots \,\!}

Последний вопрос нашей задачи можно переформулировать так: при каких значениях x{\displaystyle x} у последовательности a1=F1(x),a2=F2(x),a3=F3(x),…{\displaystyle a_{1}=F_{1}(x),\;a_{2}=F_{2}(x),\;a_{3}=F_{3}(x),\;\ldots \,\!}
есть предел, то есть существует некоторое число A{\displaystyle A}, зависящее от x{\displaystyle x}, к которому стремится последовательность ai=Fi(x){\displaystyle a_{i}=F_{i}(x)\,\!}?