Дискретное представление информации

Презентация на тему: » Двоичное кодирование текстовой информации Содержание 1.Как представляется текст в памяти компьютера.Как представляется текст в памяти компьютера. 2.КодКод.» — Транскрипт:

2

Двоичное кодирование текстовой информации

3

Содержание 1.Как представляется текст в памяти компьютера.Как представляется текст в памяти компьютера. 2.КодКод 3.Способы кодированияСпособы кодирования 4. ДекодированиеДекодирование 5. Таблица кодированияТаблица кодирования 6. Международный стандартМеждународный стандарт

4

Как представляется текст в памяти компьютера Начиная с конца 60-х годов компьютеры все больше стали использоваться для обработки текстовой информации, и в настоящее время основная доля персональных компьютеров в мире (и большая часть времени) занята обработкой именно текстовой информации.

5

Как представляется текст в памяти компьютера Давайте «заглянем» в память компьютера и разберёмся, как же представлена в нём текстовая информация?

6

Как представляется текст в памяти компьютера Текстовая информация состоит из символов: букв, цифр, знаков препинания, скобок и других. Мы думаем вы уже знаете, что множество всех символов, с помощью которых записывается текст, называется алфавитом, а число символов в алфавите – его мощностью.

7

Код Для представления текстовой информации в компьютере используется алфавит мощностью 256 символов. Вы знаете, что один символ такого алфавита несёт 8 битов информации: 2 8 = битов = 1 байт, следовательно:

8

Код Двоичный код каждого символа в компьютерном тексте занимает 1 байт памяти! Запомни !!!

9

Важно, что присвоение символу конкретного кода это вопрос соглашения, которое фиксируется в кодовой таблице. Первые 33 кода (с 0 по 32) обозначают не символы, а операции (перевод строки, ввод пробела и т

д.).

10

Код Коды с 33 по 127- интернациональные и соответствуют символам латинского алфавита, цифрам, знакам арифметических операций и знакам препинания.

11

Код Коды с 128 по 255 являются национальными, т. е. в национальных кодировках одному и тому же коду отвечают различные символы. К сожалению, в настоящее время существует пять различных кодовых таблиц для русских букв (КОИ-8, СР1251, СР866, Мае, ISO), поэтому тексты, созданные в одной кодировке, не будут правильно отображаться в другой.

12

Способы кодирования У вас может возникнуть вопрос: «Какой именно восьмиразрядный код поставить в соответствие каждому символу?»

13

Способы кодирования Каждая кодировка задается своей собственной кодовой таблицей. Одному и тому же двоичному коду в различных кодировках поставлены в соответствие различные символы.

14

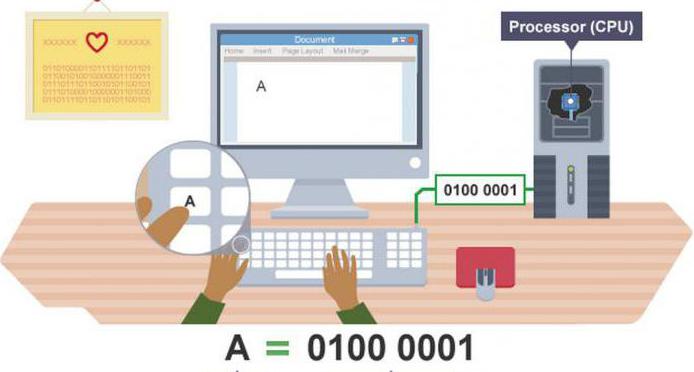
Способы кодирования При вводе в компьютер текстовой информации происходит ее двоичное кодирование, изображение символа преобразуется в его двоичный код. Пользователь нажимает на клавиатуре клавишу с символом — и в компьютер поступает определенная последовательность из восьми электрических импульсов (двоичный код символа). Код символа хранится в оперативной памяти компьютера, где занимает одну ячейку.

15

Декодирование В процессе вывода символа на экран компьютера производится обратный процесс — декодирование, т. е. преобразование кода символа в его изображение.

16

Таблица кодирования Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.

17

Для разных типов ЭВМ используются различные таблицы кодировки. С распространением персональных компьютеров типа IBM PC международным стандартом стала таблица кодировки под названием ASCII (American Standart Code For Information Interchange – американский стандартный код для информационного обмена).

18

Таблица кодирования Точнее говоря, стандартной в этой таблице является только первая половина, т. е. С номерами от нуля (двоичный код ) до 127 ( ). Сюда входят буквы латинского алфавита, цифры, знаки препинания, скобки и другие символы. Остальные 128 кодов, начиная с и кончая , используется в разных вариантах. В русских национальных кодировках в этой части таблицы размещаются символы русского алфавита.

19

Международный стандарт В последнее время появился новый международный стандарт Unicode, который отводит на каждый символ не один байт, а два, и потому с его помощью можно закодировать не 256 символов, а N = 216 = различных символов. Эту кодировку поддерживают последние версии платформы Microsoft Windows & Office (начиная с 1997 года).

20

Подготовили презентацию Ученицы (подруги на протяжении 11 лет) 11 А класса МОУ «Гимназии 6» Шутенко А.А. и Нефёдова М.Ю. Дата создания:

21

Руководитель: Свиридова И. П.

Принцип алфавитного подхода к оценке количества информации

Алфавитный подход строится на принципе, утверждающем, что любое сообщение можно представить в виде кодов с помощью конечной последовательности символов, содержащейся в любом алфавите. Носители информации содержат любые последовательности символов, которые могут храниться, передаваться и обрабатываться как с помощью человека, так и с помощью технических устройств, в частности компьютера. Этот подход описал А.Н. Колмогоров, согласно которому, информативность, заключающаяся в последовательности символов, не может зависеть от содержания самого сообщения, а может определяться лишь минимальным количеством символов, необходимых для ее кодирования. Подобный подход к оценке количества информации носит объективный характер, так как не зависит от получателя, принимающего сообщения. Смысл же сообщений может учитываться только на этапе выбора алфавита кодирования либо не учитываться совсем.

В основу принципа этого подхода лег подсчет числа символов в сообщении, таким образом, важна только длина сообщения и совсем не учитывается его содержание. Однако на длину сообщения может влиять мощность алфавита используемого языка.

Самый простой способ разобраться в этом — рассмотреть пример любого текста, написанного на каком-нибудь языке. Для нас, конечно же, удобным будет текст на русском языке.

Информационный вес символов

Однако общее понятие мощности алфавита не определяет сущности вычислений информационных объемов текста, содержащего литеры, цифры и символы. Здесь требуется особый подход.

В принципе, задумайтесь, ну вот каким может быть минимальный набор с точки зрения компьютерной системы, сколько символов он может содержать? Ответ: два. И вот почему. Дело в том, что каждый символ, будь то буква или цифра, имеет свой информационный вес, по которому машина и распознает, что именно перед ней. Но компьютер понимает лишь представление в виде единиц и нулей, на чем, собственно, и основана вся информатика.

Таким образом, любой символ можно представить в виде последовательностей, содержащих цифры 1 и 0, то есть, минимальная последовательность, обозначающая букву, цифру или символ, состоит из двух компонентов.

Сам же информационный вес, принятый за стандартную информационную единицу измерения, называется битом (1 бит). Соответственно, 8 бит составляют 1 байт.

II. Кодирование информации.

Компьютер
может обрабатывать только информацию,
представленную в числовой форме. Вся
другая информация (тексты, звуки,
изображения, показания приборов и т.д.)
для обработки на компьютере должна быть
преобразована в числовую форму.

Переход
от одной формы представления информации
к другой, более удобной для хранения,
передачи или обработки, называется
кодированием


информации.

Кодирование


– это операция преобразования знаков
или групп знаков одной знаковой системы
в знаки или группы знаков другой знаковой
системы.

Как
правило, все числа в компьютере
представляются с помощью нулей и единиц,
т.е. работа производится в двоичной
системе счисления, поскольку при этом
устройства для их обработки получаются
значительно более простыми.

Отображение символов в двоичном коде

Алфавитная мощность может быть использована на практике только при наличии двоичного кода. В качестве примера можно использовать упрощённый алфавит, состоящий всего из четырёх символов. В этом случае разрядность их и информационное представление описываются следующим образом:

• 1 — 00;
• 2 — 01;
• 3 — 10;
• 4 — 11.

Из этого списка можно сделать вывод о том, что если алфавитная мощность равняется 4, то масса отдельного единичного символа будет составлять 2 бита. Если же есть алфавит, состоящий из 8 символов, то при подборе двоичного трёхзначного кода для него комбинационное количество будет следующим:

• 1 — 000;
• 2 — 001;
• 3 — 010;
• 4 — 011;
• 5 — 100;
• 6 — 101;
• 7 — 110;
• 8 — 111.

Перевод чисел в бинарный код

Числовой способ кодирования информации, т.е. переход информационных данных в бинарную последовательность чисел широко распространен в современной компьютерной технике. Любая числовую, символьную, графическую, аудио- и видеоинформацию можно закодировать двоичными числами. Рассмотрим подробнее кодирование числовой информации.

Привычная человеку система счисления (основанная на цифрах от 0 до 9), которой мы активно пользуемся, появилась несколько сотен тысяч лет назад. Работа всей вычислительной техники организована на бинарной системе счисления. Алфавитом у нее минимальный – 0 и 1. Кодировка чисел совершается путем перехода из десятичной в двоичную систему счисления и выполнении вычислений непосредственно с бинарными числами.

Кодирование и обработка числовой информации обусловлено желаемым результатом работы с цифрами. Так, если число вводится в рамках текстового файла, то оно будет иметь код символа, взятого из используемого стандарта. Для математических вычислений числовые данные преобразуются совершенно другим способом.

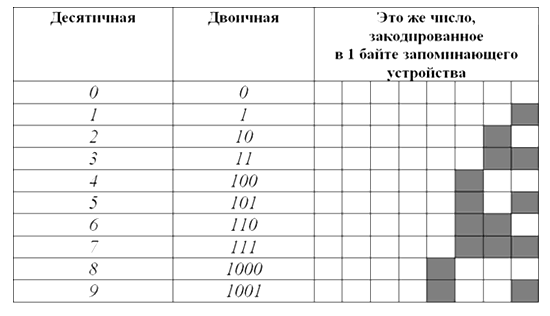
Принципы кодирования числовой информации, представленной в виде целых или дробных чисел (положительных, отрицательных или равных 0) отличаются по своей сути. Самый простой способ перевести целое число из десятичной в двоичную систему счисления заключается в следующем:

1. число нужно разделить на 2;
2. если частное больше 1, то необходимо продолжить деление до того момента, пока результат будет равен 0 или 1;
3. записать результат последней операции и остатки от деления в обратной последовательности;
4. полученное число и будет являться искомым кодовым значением.

Одна из важнейших частей компьютерной работы – кодирование символьной информации. Все многообразие цифр, русских и латинских букв, знаков препинания, математических знаков и отдельных специальных обозначений относятся к символам. Cимвольный способ кодирования состоит в присвоении определенному знаку установленного шифра.

Источник

Рассмотрим подробнее самые распространенные стандарты ASCII и Unicode – то, что применяется для кодирования символьной информации во всем мире.

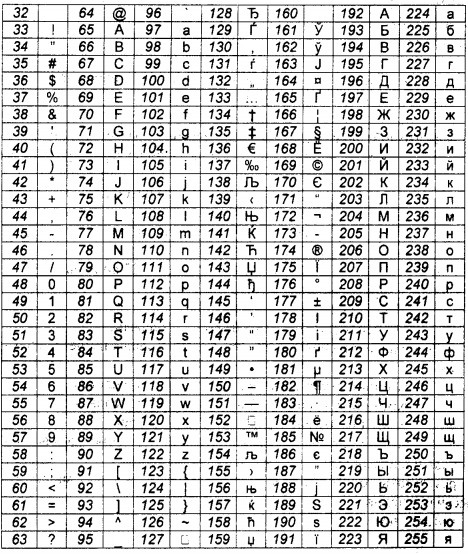Фрагмент таблицы ASCII

Первоначально было установлено, что для любого знака отводится в памяти компьютера 8 бит (1 бит – это либо «0», либо «1») бинарной последовательности. Первая таблица кодировки ASCII (переводится как «американский кодовый стандарт обмена сообщениями») содержала 256 символов. Ограниченная численность закодированных знаков, затрудняющая межнациональный обмен данными, привела к необходимости создания стандарта Unicode, основанного на ASCII. Эта международная система кодировки содержит 65536 символов. Закодировать огромное количество всевозможных обозначений стало возможным благодаря использованию 16-битного символьного кодирования.

Кодирование символьной и числовой информации принципиально отличается. Для ввода-вывода цифр на монитор или использовании их в текстовом файле происходит преобразование их согласно системе кодировки. В процессе арифметических действий число имеет совершенно другое бинарное значение, потому что оно переходит в двоичную систему счисления, где и совершаются все вычислительные действия.

Выбирать способ кодирования информации – графический, числовой или символьный необходимо отталкиваясь от цели кодировки. Например, число «21» можно ввести в компьютерную память цифрами или буквами «двадцать один», слово «ЗИМА» можно передать русскими буквами «зима» или латинскими «ZIMA», штрих-код товара передается изображением и цифрами.

Двоичный код

Самый широко используемый метод кодирования информации – двоичное кодирование. Кодирование данных двоичным кодом применяется во всех современных технологиях.

Двоичный (бинарный) код — последовательность нолей и единиц. Это универсальный способ отображения любых информационных сведений (текстовых сообщений, картинок, звуковых и видеоматериалов). Сведения, закодированные в бинарном коде, очень удобно хранить, обрабатывать и передавать с одного электронного устройства на другое, в чем и заключается преимущества использования двоичного кодирования информации.  

Двоичное кодирование информации применяется для различных данных:

• двоичное кодирование текстовой информации заключается в присвоении буквенным, цифровым и другим обозначениям определенного кода. Он записывается в компьютерной памяти цепочкой из нулей и единиц. Порядок кодирования алфавита в двоичный код с помощью стандарта ASCII является наглядным примером;
• вид используемой графики влияет на то, каким образом производится двоичное кодирование графической информации;
• двоичное кодирование звуковой информации происходит после дискретизации звуковой волны и присвоения каждому компоненту соответствующего бинарной цепочки чисел;
• кодирование двоичным кодом видеоматериалов сочетает принципы работы со звуком и растровыми изображениями.

РЕШЕНИЕ ЗАДАЧ

При хранении и передаче информации с помощью технических устройств информацию следует рассматривать как последовательность символов — знаков (букв, цифр, кодов цветов точек изображения и т.д.).

N=2 i	i	Информационный вес символа, бит
N	Мощность алфавита
I=K*i	K	Количество символов в тексте
I	Информационный объем текста

Возможны следующие сочетания известных (Дано) и искомых (Найти) величин:

Тип	Дано	Найти	Формула
1	i	N	N=2 i
2	N	i
3	i,K	I	I=K*i
4	i,I	K
5	I, K	i
6	N, K	I	Обе формулы
7	N, I	K
8	I, K	N

Задача 1. Получено сообщение, информационный объем которого равен 32 битам. чему равен этот объем в байтах?

Решение: В одном байте 8 бит. 32:8=4 Ответ: 4 байта.

Задача 2. Объем информацинного сообщения 12582912 битов выразить в килобайтах и мегабайтах.

Решение: Поскольку 1Кбайт=1024 байт=1024*8 бит, то 12582912:(1024*8)=1536 Кбайт и поскольку 1Мбайт=1024 Кбайт, то 1536:1024=1,5 Мбайт Ответ:1536Кбайт и 1,5Мбайт.

Задача 3. Компьютер имеет оперативную память 512 Мб. Количество соответствующих этой величине бит больше:

1) 10 000 000 000бит 2) 8 000 000 000бит 3) 6 000 000 000бит 4) 4 000 000 000бит Решение: 512*1024*1024*8 бит=4294967296 бит. Ответ: 4.

Задача 4. Определить количество битов в двух мегабайтах, используя для чисел только степени 2. Решение: Поскольку 1байт=8битам=2 3 битам, а 1Мбайт=2 10 Кбайт=2 20 байт=2 23 бит. Отсюда, 2Мбайт=2 24 бит. Ответ: 2 24 бит.

Задача 5. Сколько мегабайт информации содержит сообщение объемом 2 23 бит? Решение: Поскольку 1байт=8битам=2 3 битам, то 2 23 бит=2 23 *2 23 *2 3 бит=2 10 2 10 байт=2 10 Кбайт=1Мбайт. Ответ: 1Мбайт

Задача 6. Один символ алфавита «весит» 4 бита. Сколько символов в этом алфавите? Решение: Дано:

i=4	По формуле N=2 i находим N=2 4 , N=16
Найти: N — ?

Ответ: 16

Задача 7. Каждый символ алфавита записан с помощью 8 цифр двоичного кода. Сколько символов в этом алфавите? Решение: Дано:

i=8	По формуле N=2 i находим N=2 8 , N=256
Найти:N — ?

Ответ: 256

Задача 8. Алфавит русского языка иногда оценивают в 32 буквы. Каков информационный вес одной буквы такого сокращенного русского алфавита? Решение: Дано:

N=32	По формуле N=2 i находим 32=2 i , 2 5 =2 i ,i=5
Найти: i— ?

Ответ: 5

Задача 9. Алфавит состоит из 100 символов. Какое количество информации несет один символ этого алфавита? Решение: Дано:

N=100	По формуле N=2 i находим 32=2 i , 2 5 =2 i ,i=5
Найти: i— ?

Ответ: 5

Задача 10. У племени «чичевоков» в алфавите 24 буквы и 8 цифр. Знаков препинания и арифметических знаков нет. Какое минимальное количество двоичных разрядов им необходимо для кодирования всех символов? Учтите, что слова надо отделять друг от друга! Решение: Дано:

N=24+8=32	По формуле N=2 i находим 32=2 i , 2 5 =2 i ,i=5
Найти: i— ?

Ответ: 5

Задача 11. Книга, набранная с помощью компьютера, содержит 150 страниц. На каждой странице — 40 строк, в каждой строке — 60 символов. Каков объем информации в книге? Ответ дайте в килобайтах и мегабайтах Решение: Дано:

K=360000	Определим количество символов в книге 150*40*60=360000. Один символ занимает один байт. По формуле I=K*iнаходим I=360000байт 360000:1024=351Кбайт=0,4Мбайт
Найти: I— ?

Ответ: 351Кбайт или 0,4Мбайт

Задача 12. Информационный объем текста книги, набранной на компьютере с использованием кодировки Unicode, — 128 килобайт. Определить количество символов в тексте книги. Решение: Дано:

I=128Кбайт,i=2байт	В кодировке Unicode один символ занимает 2 байта. Из формулыI=K*i выразимK=I/i,K=128*1024:2=65536
Найти: K— ?

Ответ: 65536

Задача 13.Информационное сообщение объемом 1,5 Кб содержит 3072 символа. Определить информационный вес одного символа использованного алфавита Решение: Дано:

I=1,5Кбайт,K=3072	Из формулы I=K*i выразимi=I/K,i=1,5*1024*8:3072=4
Найти: i— ?

Ответ: 4

Задача 14.Сообщение, записанное буквами из 64-символьного алфавита, содержит 20 символов. Какой объем информации оно несет? Решение: Дано:

N=64, K=20	По формуле N=2 i находим 64=2 i , 2 6 =2 i ,i=6. По формуле I=K*i I=20*6=120
Найти: I— ?

Ответ: 120бит

Задача 15. Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если его объем составил 1/16 часть мегабайта? Решение: Дано:

N=16, I=1/16 Мбайт	По формуле N=2 i находим 16=2 i , 2 4 =2 i ,i=4. Из формулы I=K*i выразим K=I/i, K=(1/16)*1024*1024*8/4=131072
Найти: K— ?

Ответ: 131072

Задача 16. Объем сообщения, содержащего 2048 символов,составил 1/512 часть мегабайта. Каков размер алфавита, с помощью которого записано сообщение? Решение: Дано:

Примеры решения задач по информатике

Определение информационного объёма в тексте

Почти всегда при наборе текста на компьютерах и других электронных устройствах приходится сталкиваться с написанием различных символов. К ним следует отнести:

• заглавные и жирные буквы;
• курсив;
• скобки;
• знаки препинания;
• вычислительные операции и прочее.

Размер любой напечатанной фразы может быть вычислен по формуле V=K ⋅ log2N. В этом случае N обозначает количество всех символов в алфавите, а K — это численность знаков непосредственно в напечатанной фразе. Так, например, имеется произвольный текст объёмом в 25 листов. На каждом из них расположено по 45 строчек текста, содержащих по 58 символов.

Исходя из этого, на любой отдельной странице будет 45*58 = 2610 байт информации. В целом же по всему тексту этот объём будет равен 2610*25 = 65250 байт. Для обозначения мощности алфавита в информатике общепринятым вариантом является буква N из формулы Хартли. Именно ее чаще всего указывают в большинстве учебников и профессиональной литературе.

В кодовой таблице ASCII используют восьмибитную кодировку текстовых сообщений. Она позволяет полностью вместить основной набор символов кириллического и латинского алфавитов как в строчном, так и в прописном вариантах. Также с её помощью можно отобразить знаки препинания, цифры и прочие базовые знаки. Часто пользователям приходится иметь дело с более крупными объёмами, состоящими из триллионов байтов.

Поскольку один отдельный символ состоит из 8 битов, то устанавливать их кодировку целиком не представляется возможным. Вместо этого предпочтительнее образовать кодировку трёхбитовых комбинаций. Расчёт этого действия проводится по формуле Хартли, где n-ная степень будет равняться трём. В результате получается N, равная 8.

При определении мощности чаще всего используют алфавитный подход. Он говорит о том, что объём информации, заложенной в тексте, зависит исключительно от мощности самого алфавита и размера сообщения (то есть количества символов, содержащихся в нём). Этот показатель не имеет никакой связи со смысловым наполнением для человека.

Мощность алфавита и информационная емкость. Формула Хартли

Все множество символов, из которых состоит язык, можно традиционно назвать алфавитом. Как правило, под алфавитом понимаются только буквы, но кроме них при написании текстов используются знаки препинания, цифры, скобки, пробелы, их тоже, в свою очередь, можно включить в алфавит.

Таким образом, алфавит — это множество символов, используемых при записи текста.

Мощность (размер) алфавита — это полное количество символов в алфавите.

Мощность алфавита обозначается буквой $N$.

Например:

• мощность алфавита, состоящего из русских букв (кириллицы), равна $33$;

• мощность алфавита, состоящего из латинских букв — $26$;

• мощность алфавита текста набранного с клавиатуры компьютера равна $256$ (строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, скобки, знаки препинания и т.д.);

• мощность двоичного алфавита равна $2$.

При алфавитном подходе считают, что каждый символ текста несет в себе определенную информационную емкость, которая, в свою очередь, зависит от мощности алфавита.

Алфавит, с помощью которого записывается сообщение, состоит из $N$ знаков. В самом простом случае при длине кода сообщения, равной одному знаку, отправитель может послать одно из $N$ возможных сообщений, которое будет нести количество информации, равное $I$, согласно формуле:

$N = 2^I$ ,

где $N$ — количество знаков в алфавите знаковой системы,

$I$ — количество информации, которое несет каждый знак.

Данную формулу вывел Р. Хартли, который в $20$-е годы прошлого столетия заложил основы теории информации, в которой определялась мера количества информации при решении некоторых задач.

Хартли утверждал, что на количество информации, содержащейся в сообщении, может влиять фактор неожиданности, который, в свою очередь, зависит от вероятности получения сообщения. Если эта вероятность получения сообщения высокая, а неожиданность при этом низкая, то сообщение будет содержать мало полезной для человека информации.

Замечание 1

Однако при создании своей формулы Р.Хартли полностью исключил фактор неожиданности. Формула Хартли работает только в том случае, когда появление символов равновероятно и они статистически независимы.

Например, с помощью приведенной формулы можно определить количество информации, которое несет знак в двоичной системе счисления:

Рисунок 1.

Информационная емкость знака двоичной системы составляет 1 бит.

Пример 1

Необходимо определить информационную емкость буквы русского алфавита (без учета буквы «ё»).

Решение:

Представим себе, что текст к нам поступает последовательно, по одному знаку, словно бумажная лента, выползающая из телеграфного аппарата. Предположим, что каждый символ, который появляется на ленте, с равной вероятностью может быть любым символом алфавита. В действительности это не совсем так, но для упрощения примем такое предположение.

В каждой очередной позиции текста может появиться любой из $N$ символов. Тогда, согласно известной нам формуле, каждый такой символ несет количество информации равное $I$ бит, которое можно определить из решения уравнения:

Рисунок 2.

Информационная емкость буквы русского алфавита составляет $5$ бит информации.

Таким образом, формула определения $N$ связывает между собой количество возможных событий и количество информации, которое содержит в себе полученное сообщение. В рассматриваемой выше задаче $N$ — это количество знаков в русском алфавите, а $I$ — количество информации, которое несёт одна буква.

Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.

Количество информации в сообщении можно определить, используя формулу:

$I_c = K \cdot I$,

где $I_c$ — количество информации, содержащееся в сообщении;

$I$ — количество информации, которое несет один знак (информационная емкость);

$K$ — количество знаков в сообщении.

Кодирование текстовой информации.

На сегодняшний день большое колличество пользователей при помощи компьютера обрабатывает текстовую информацию, которая состоит из: букв, цифр, знаков препинания и других элементов.

Обычно для кодирования одного символа, используеться 1 байт памяти то есть 8 бит. По теории вероятностей с помощью простой формулы, которая связывает количество возможных событий (К) и количество информации (I), можно вычислить сколько не одинаковых символов можно закодировать: К = 2^I = 28 = 256.

Примечание

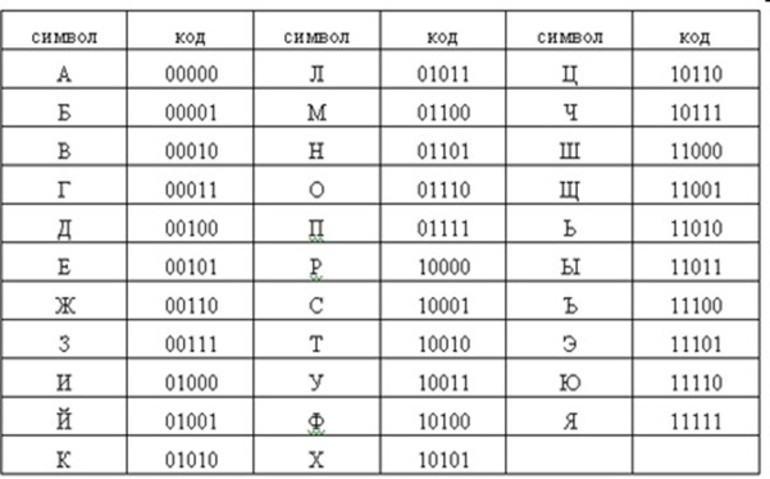
Принцип данного кодирования заключается в том, что каждому символу (букве, знаку) соответствуе свой двоичный код от 00000000 до 11111111, так-же текстовая информация может быть представлена в десятичном коде от 0 до 255.

Нужно запомнить, что на сегодняшний день для кодирования букв российского алфавитаиспользуют пять разных кодировачных таблиц (КОИ — 8, СР1251, СР866, Мас, ISO), запомните, что тексты закодированные с помощью одной таблицы не будут корректно отображаться в другой кодировке. Это можно увидить в обьединенной таблице кодировки символов.

Для одного двоичного кода в разных таблицах соответствуют разные символы:

Двоичный код	Десятичный код	КОИ8	СР1251	СР866	Мас	ISO
11000010	194	б	В	—	—	Т

На сегодняшний день перекодированием текстовых документов заботится не пользователь, а программы, которые встроены в текстовые редакторы и текстовые процессоры. В начале 1997 года Microsoft Office начали поддерживать новую кодировку Unicode. В Unicode можно закодировать не 256 символов а, 65536, это было достигнуто тем, что под каждый символ начали отводить 2 байта. Сегодня больше всего популярны две таблицы это Windows (СР1251), и Unicode.

Решаем задачи.

Задача №1.
Допустим у нас есть два текста которые содержат одинаковое колличество символов. Один текст записан на русском языке его алфавит (32 символа), а второй допустим на украинском его алфавит (16 символов). Чей текст несет большее количество информации?

Задача №2.Объем сообщения, содержащего 2048 символов, составил 1/512 часть Мбайта. Определить мощность алфавита.

Почему терабайтный диск вмещает 900 ГБ?

Производители винчестеров умело пользуются малой осведомленностью некоторых пользователей. Так, практически каждый покупатель нового HDD после форматирования обнаруживал, что вместо обещанного 1 ТБ система показывает чуть больше 900 ГБ свободного места на носителе. В результате многие пользователи начинают интересоваться, куда пропадают почти 10% объема жесткого диска.

Секрет кроется в том, что производители HDD во время измерения объема дисков используют не двоичную, а десятичную систему. Другими словами, они при подсчетах принимают 1 килобайт за тысячу байт. В результате разница составляет 24 единицы измерения информации. Если же учитывать достаточно большой объем жесткого диска, то производитель остаются в выигрыше, так как разница увеличивается уже в десятки гигабайт.

Если бы каждый из производителей HDD использовал правильный подсчет объема дисков, тогда 1 ГБ равен был бы 107374824 байт. При пересчете в терабайт нужно данное значение еще умножить на 1024. В результате терабайтный диск вмещал бы 109951819776 байт.

Теперь вы знаете, как определяют производители объем памяти выпущенных устройств. Они используют очень простой трюк, чтобы всегда оставаться в выигрыше. При этом потребители приобретают товар, полезность которого на 10% меньше.

Здравствуйте, уважаемые читатели блога сайт! В условиях бурного развития информационных технологий недурственно бы получить знания по некоторым фундаментальным аспектам, хотя бы основным. Это может оказать серьезную помощь в дальнейшем.

В интернете, которым мы пользуемся благодаря компьютерам, вся информация хранится или передается в закодированном цифровом формате, а потому должны обязательно существовать способы измерить объем этих данных, ведь от этого зависит системность работы с ними. Такими единицами измерения служат бит и байт.

По аналогии с известными нам физическими единицами измерения, которые при большой их величине для удобства исчисления получают увеличительные приставки (1000 метров = 1 километр, 1000 грамм = 1 килограмм), единица информации байт тоже имеет свои производные (килобайт, мегабайт, гигабайт и т.д.). Однако, в случае бита и байта существуют нюансы, о которых я подробнее и поведаю.