Сад. распределения

Доступные размещения с повторениями и без них

Работа с различными математическими комбинациями подразумевает использование определённых правил, в противном случае избежать распространённых ошибок будет крайне сложно. Если имеющаяся l различных элементов может повториться m раз, оказавшись на имеющихся m местах, тогда при составлении вывода количество размещений с последующими повторениями вычисляется по определённой комбинаторной формуле — Am / l = lm. Именно под этим определением принято понимать чёткий набор компонентов m из множества l: A m/l = l * (l-1) * (l -2) *… * (l—m +1) = l!/(l—m)!.

Изучаемое число сочетаний без повторений сопряжено с некоторыми дополнительными нюансами. В этом случае в распоряжении учащегося имеется n разных математических элементов. Многих в такой ситуации интересует, сколько именно можно будет составить актуальных k расстановок.

Два базовых подхода считаются различными только при условии, если они отличаются друг от друга минимум одним элементом или состоят из аналогичных элементов, которые расположены в разном порядке. Каждый нюанс должен быть учтён, так как от этого зависит итоговый результат.

Изучаемые в этом случае расстановки указывают на право размещения без повторений, а вот их число обозначают как Ak / n (читается следующим образом: а из n по k). Первая буква является неотъемлемым элементом довольно известного французского слова Arrangement, которое означает «приведение в порядок». В такой ситуации популярность получила следующая формула: Ak / l = l (l -1) * (l -2)… (l — k +1). Специальные комбинации позволяют определить даже автомобильный региональный код.

Описанные правила и формулы позволяют решать довольно сложные и многоуровневые задачи. К примеру, из трёх предъявленных цифр нужно выбрать только две, чтобы в итоге получились разные двузначные числа. По условиям описанной задачи нужно определить, сколько вариантов существует в этом случае. Ответ: (4а) А2/3=3*2 = 6. Но также уместно следующее решение: А2/3 = 3!/(3−2)! = 3!/1! = 1*2*3/1 = 6. В этом случае каждый существующий элемент может быть расположен по несколько раз, что соответствует условиям задачи. Для этой ситуации уместна следующая формула: (5) Ak / l = lk.

Непрерывное равномерное распределение

Простейший пример непрерывной случайной величины — непрерывная случайная величина с равномерным распределением между числами и . Назовём её . Пишут  (англ. Uniform — равномерный).
 
Обычно равномерным распределением описывают процессы, о которых мало информации или в целом нет причин предполагать сложную зависимость. Например:

• -метровый провод повреждён, но в какой именно точке — неизвестно. Видно, что на первых двух метрах всё в порядке, как и на последних трёх. Оставшаяся средняя часть провода скрыта за плинтусом. У электрика нет более точной информации о местоположении повреждения, то есть оно с равной вероятностью может располагаться в любом месте скрытого промежутка. Поэтому подходит равномерное распределение с  и . Значит, здесь .
• Николай ждёт звонка с  до . Звонок происходит в случайный момент, то есть с равной вероятностью от начала периода может пройти любое время. Здесь .
• Турист ждёт поезд в метро. Турист не знает города, поэтому считает, что поезда приходят в случайное время. По разговорам людей турист понял, что поезд в метро всегда приходит в течение  минут. Он с равной вероятностью может прождать любой промежуток времени до  минут. Здесь .

График плотности вероятности для будет выглядеть так:

Функция плотности вероятности для непрерывного равномерного распределения равна нулю везде, кроме отрезка . На отрезке  она равна , потому что общая площадь под графиком должна быть равна . Аналогичное верно и для дискретных распределений: сумма вероятностей всех значений должна быть равна .
 
Проверим, что площадь под функцией плотности вероятности для непрерывного равномерного распределения равна . Эта площадь равна площади прямоугольника с длиной, равной длине отрезка , и высотой, равной . Получаем: , что и было нужно!
 
Используем функцию плотности вероятности, чтобы найти вероятность того, что попадёт в конкретный интервал. Рассмотрим задачу.
 
Программист Никита решает рабочую задачу за время от двух до пяти часов, причём с одинаковой вероятностью на случайную задачу он тратит любое время из этого промежутка и никогда — меньше двух или больше пяти часов. Значит, это равномерное распределение с  и  то есть .
 
Вычислим при таких и   Значит, график плотности вероятности выглядит так:

Определим, чему равна вероятность того, что Никита потратит на решение следующей задачи из бэклога от двух до четырёх часов? Вероятность того, что  попадёт в интервал , равна площади под графиком над этим отрезком:

ИНДЕКС ПОИСКПОЗ поиск по нескольким столбцам – пример формулы

В этом примере мы будем использовать таблицу с комбинацией критериев (в нашем случае регион-месяц-товар) в каждой строке. Наша цель — получить данные о продажах определенного товара в данном регионе и в нужном месяце.

Вот наши исходные данные и критерии:

• Диапазон_возврата (продажи) — D2:D13
• Критерий1 (целевой регион) – G1
• Критерий2 (целевой месяц) – G2
• Критерий 3 (целевой товар) — G3
• Диапазон1 (регионы) – A2:A13
• Диапазон2 (месяцы) – B2:B13
• Диапазон3 (товары) – C2:C13

Формула принимает следующий вид:

Запишем формулу в G4, завершим ее, нажав Получаем следующий результат:

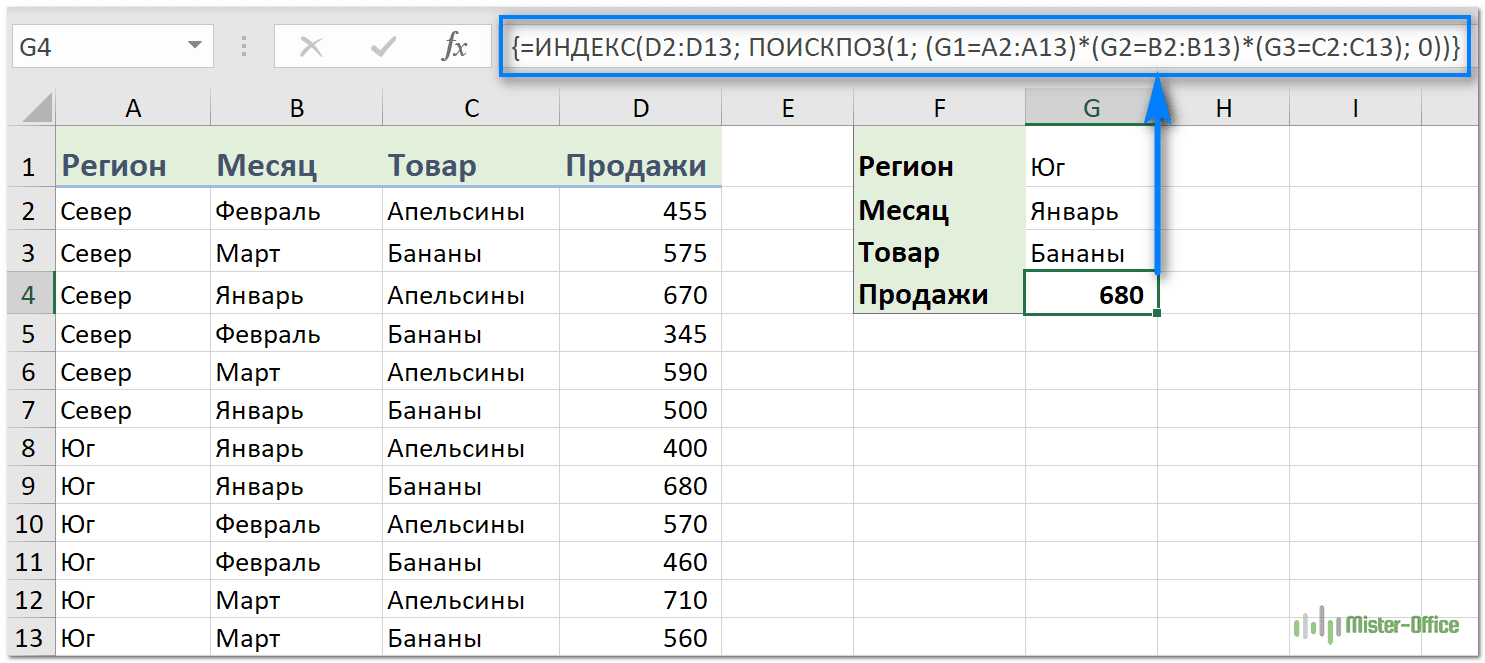
Как это работает? Разберем пошагово.

Самая сложная часть — это функция ПОИСКПОЗ, так что давайте пошагово рассмотрим логику ее работы:

ПОИСКПОЗ(1; (G1=A2:A13)*(G2=B2:B13)*(G3=C2:C13)

Как вы помните, ПОИСКПОЗ ищет заданное значение в массиве и возвращает относительное его положение в этом массиве.

В нашей формуле аргументы следующие:

• Искомое_значение : 1
• Массив поиска : (G1=A2:A13) * (G2=B2:B13) * (G3=C2:C13)
• Тип_соответствия : 0

Шаг 1.

Первый аргумент предельно ясен — функция ищет число 1. Третий аргумент, установленный в 0, означает «точное совпадение», т.е. формула возвращает первое найденное значение, которое точно равно искомому значению.

Вопрос в том, почему мы ищем «1»? Чтобы получить ответ, давайте внимательнее посмотрим на массив поиска, где мы сравниваем каждый наш критерий с соответствующим диапазоном: целевой регион в ячейке G1 со всеми регионами (A2: A13), целевой месяц в G2 со всеми месяцами (B2: B13), и товар в G3 в колонке товаров (C2:C13). В результате этих сравнений мы имеем 3 массива значений ИСТИНА и ЛОЖЬ, где ИСТИНА представляет значения, соответствующие условию. Чтобы визуализировать это, вы можете выбрать отдельное выражение в формуле и нажать клавишу F9 , чтобы увидеть, что оно возвращает:

=ИНДЕКС(D2:D13; ПОИСКПОЗ(1; {ЛОЖЬ:ЛОЖЬ:ЛОЖЬ:ЛОЖЬ:ЛОЖЬ:ЛОЖЬ:ИСТИНА:ИСТИНА:ИСТИНА:ИСТИНА:ИСТИНА:ИСТИНА}*{ЛОЖЬ:ЛОЖЬ:ИСТИНА:ЛОЖЬ:ЛОЖЬ:ИСТИНА:ИСТИНА:ИСТИНА:ЛОЖЬ:ЛОЖЬ:ЛОЖЬ:ЛОЖЬ}*{ЛОЖЬ:ИСТИНА:ЛОЖЬ:ИСТИНА:ЛОЖЬ:ИСТИНА:ЛОЖЬ:ИСТИНА:ЛОЖЬ:ИСТИНА:ЛОЖЬ:ИСТИНА}; 0))

Шаг 2.

Операция умножения преобразует значения ИСТИНА и ЛОЖЬ в 1 и 0 соответственно:

{0:0:0:0:0:0:1:1:1:1:1:1}*{0:0:1:0:0:1:1:1:0:0:0:0}*{0:1:0:1:0:1:0:1:0:1:0:1}

Шаг 3.

А поскольку умножение на 0 всегда дает 0, результирующий массив содержит 1 только в тех строках, которые соответствуют всем трём условиям:

{0:0:0:0:0:0:0:1:0:0:0:0}

Приведенный выше массив переходит в аргумент массив_поиска функции ПОИСКПОЗ. Функция возвращает порядковый номер позиции с цифрой 1, для которой все критерии имеют значение ИСТИНА (строка 8 в нашем случае). Если в массиве будет несколько единиц, будет определена позиция только первой из них.

Шаг 4.

Число, возвращаемое функцией ПОИСКПОЗ, поступает непосредственно в аргумент номер_строки функции ИНДЕКС(массив, номер_строки, ):

=ИНДЕКС(D2:D13,

И это дает результат 680, что является восьмым по счету значением в массиве D2:D13.

Расчёт вероятности определённого порядка успехов и неуспехов

Для начала посмотрим, как находить вероятности того, что в биномиальном эксперименте успехи и неудачи произойдут в определённом порядке. Например, в эксперименте с кликами пользователей — вероятность того, что из пяти независимо кликающих по баннеру пользователей первые три попадут по баннеру, а следующие двое промажут. В эксперименте с питонами это может быть вероятность того, что два первых питона из трёх будут добрыми, а последний — злым.
 
Найти эту вероятность нам поможет правило:
 

Если события независимы, вероятность того, что они произойдут вместе, равна произведению их вероятностей.
 

Как сделать поиск с несколькими условиями

При работе с большими базами данных вы можете иногда оказаться в ситуации, когда нужно что-то найти, но нет единственного уникального идентификатора для поиска, критериев много. В этом случае поиск с несколькими условиями является единственным решением.

Чтобы найти значение на основе нескольких критериев в отдельных столбцах, используйте эту общую формулу:

Где:

• Диапазон_возврата — это диапазон, из которого возвращается значение.
• Критерии1 , критерии2 , … – это условия, которые необходимо выполнить.
• Диапазон1 , диапазон2 , … — это диапазоны, на которых должны проверяться соответствующие критерии.

Важное замечание! Это формула массива , и она должна быть введена через . Появятся {фигурные скобки}, что является визуальным признаком формулы массива в Excel. Не пытайтесь вводить фигурные скобки вручную, это не сработает!

Эта формула представляет собой расширенную версию комбинации ИНДЕКС+ПОИСКПОЗ, которая возвращает совпадение на основе одного критерия. Чтобы оценить несколько условий, мы используем операцию умножения, которая работает как оператор «И» в формулах массива . Ниже вы найдете реальный пример и подробное пошаговое объяснение логики расчетов.

Условие хорошей аппроксимации

Теперь сформулируем условие хорошей аппроксимации:
 

Нужно взять промежуток от математического ожидания биномиального распределения плюс-минус три его стандартных отклонения. Если он лежит в пределах  (то есть там, где биномиальное распределение определено), то его форма будет симметрична и близка к нормальному распределению.
 

И наоборот: если промежуток от мат.ожидания биномиального распределения плюс-минус три его стандартных отклонения выходит за пределы , график биномиального распределения будет скошенным. Значит, симметричная кривая нормального распределения не даст хорошей аппроксимации.
 
Чем дальше от  — то есть чем ближе к  или , — тем ближе мат.ожидание  будет к краям промежутка . Поэтому условием аппроксимации часто считают , близкое к . Мы покажем, почему эта формулировка неудачна. Сформулированное выше условие работает лучше: если  достаточно велико,  может быть равно и  и , и даже  — аппроксимация всё равно будет хорошей.

Топ вопросов за вчера в категории Информатика

Информатика 02.07.2023 00:01 977 Асеев Никита

12. Назначение антивирусных программ под названием «детекторы: а) обнаружение и уничтожение

Ответов: 2

Информатика 19.02.2019 02:06 69 Ильин Кирилл

1) Программное обеспечение (ПО) – это: а)совокупность программ, позволяющих организовать решение

Ответов: 3

Информатика 29.04.2023 14:47 1950 Котик Даша

Укажите тип файла fact.exe. 1) текстовый    2) графический    3) исполняемый    4) Web-страница 

Ответов: 2

Информатика 13.07.2023 14:13 3 Медведева Диана

Написать программу на любом из предложенных языков программирование (pascal, basic C++. Phyton)С

Ответов: 2

Информатика 22.07.2018 15:40 21 Котик Даша

СРЧНО По каким признакам мы сравниваем реальные объекты? 1) по существенным признакам 2) по

Ответов: 2

Информатика 04.05.2019 07:42 19 Акулов Илья

Команда формируется:а. в арифметико-логическом устройствеб. в основной памятив. в устройстве

Ответов: 2

Информатика 28.06.2023 12:02 5 Государева Анна

А) Як встановити надбудову Аналіз даних у середовищі табличного процесора? б) Які фінансові

Ответов: 2

Информатика 06.11.2023 09:16 12 Гнатишина Элеонора

Python. Даны длины катетов прямоугольного треугольника. вычислить его периметр и площадь при выводе

Ответов: 2

Информатика 16.06.2023 15:58 12 Самойлова Лиза

Выберите допустимое для языка Python выражение: Выберите один вариант ответа _test1 = a + b Test

Ответов: 2

Информатика 02.08.2020 08:13 73 Остроушко Юлия

Вычислите: CCXLI + CXXXVI результат запишите в Римской системе счисления

Ответов: 1

Функция распределения Пуассона

В модуле есть ещё один метод: . Он выдаёт значения функции распределения для распределения Пуассона, то есть суммарную вероятность значений от  до заданного. Построим с его помощью график функции вероятности для того же распределения с параметром . Отобразим значения функции вероятности для первых  целых значений, на которых определено распределение Пуассона.

Получим следующий график:

Сотрудники пляжа в среднем находят в неделю  потерянных солнцезащитных очков, владельца которых так и не удаётся найти. Местная экологическая компания готова взять на переработку партию от  солнечных очков. Какова вероятность, что за календарное лето сотрудники пляжа найдут достаточно очков, чтобы сдать их в переработку?
 
В задаче дана интенсивность в неделю, а нужно рассчитать вероятность за календарное лето — это другой временной отрезок. Чтобы решить эту задачу, используем свойство распределения Пуассона, которое позволяет масштабировать интенсивность.
 
План решения такой:

1. Рассчитаем количество недель в календарном лете.
2. Умножим количество недель на интенсивность событий в неделю. Так мы получим параметр, который задаёт нужное распределение.
3. Найдём вероятность с помощью метода :
   • В задаче нужно найти вероятность правого «хвоста». Метод помогает получить вероятность левого. Поэтому найдём вероятность левого и вычтем её из единицы — так получим нужную вероятность правого «хвоста».
   • В метод передадим минимальное количество найденных очков, уменьшенное на единицу: чтобы получить суммарную вероятность значений от и выше, из единицы нужно вычесть суммарную вероятность значений до включительно.

Получаем код:

Результат:

 — почти две трети, немало. А если добавить к  дней сентября, получится больше . Если что, заботящиеся об экологии сотрудники пляжа могут рассчитывать на бархатный сезон.

Теперь менеджер знает, что за месяц из  дней можно ожидать включения дополнительного электрогриля.

Корректность моделирования

Вспомним фотографию с ростом студентов.
Рост  студентов считают нормально распределённой случайной величиной. Строго говоря, мы имеем дело с конечным набором чисел, но описываем его с помощью непрерывной случайной величины. Более того, нормальное распределение определено на всей числовой оси, но не существует людей с отрицательным ростом или десятиметровых. Почему же всё равно используют эту модель?
 
Если взять нормальное распределение роста  и рассчитать вероятность того, что  окажется отрицательным, получится примерно . Это исчезающе малая вероятность, которой можно пренебречь.
 
Утверждение, что набор данных распределён нормально, предполагает допущение. Любая математическая модель приблизительна, она может быть более или менее удачной для конкретной задачи. Модель — это инструмент, и, если понимать его возможности и цели, он отлично помогает.
 
И последнее замечание. Гистограмма частот значений нормально распределённой величины не всегда идеально соответствует теоретической кривой плотности вероятности. Возможны небольшие отклонения, — как например, на уже упомянутой фотографии. Приведём несколько гистограмм частот для переменной, значения которой случайно сгенерированы из одного и того же нормального распределения. Как видите, они могут заметно отличаться, но это всё еще графики для случайной величины, имеющей одно и то же нормальное распределение.

Как рассчитывать вероятности с помощью аппроксимации

Когда мы говорили о непрерывных распределениях, например о нормальном, мы утверждали, что вероятность любого конкретного значения непрерывной переменной равна нулю. Значит, нужно отвечать на вопрос, какова вероятность для непрерывной переменной попасть в какой-либо промежуток. Напомним: эта вероятность равна площади под графиком плотности вероятности над этим промежутком.
 
Как же тогда использовать непрерывную аппроксимацию для дискретного распределения? Это делают так: чтобы найти приблизительную вероятность значения биномиальной величины, берут вероятность того, что аппроксимирующая её нормальная величина попадёт в соответствующий этому значению промежуток. Например, для значения  это будет промежуток .
 
Возьмём биномиально распределённую случайную величину . Построим для неё аппроксимацию нормальным распределением:
 

 
Значит, нормально распределённая случайная величина, аппроксимирующая , имеет распределение .
Вот графики  и :

Вероятность произвольного числа успехов из произвольного числа повторений испытания Бернулли

Пусть мы провели  экспериментов по схеме Бернулли, вероятность успеха в которой равна Нас интересует вероятность получить  успехов Действуем по той же схеме, что и для двух и трёх экспериментов. Получаем такой алгоритм:
 
Чтобы найти вероятность получить  успехов из  экспериментов по схеме Бернулли, надо:

1. Перемножить вероятности всех успехов и неудач. Каждый исход состоит из успехов и  неудач. Вероятность успеха равна  всего их  штук, значит, вероятность всех успехов равна  Вероятность неудачи равна всего их  штук, значит, вероятность всех неудач Получаем вероятность исхода с успехами из испытаний:
2. Вычислить число исходов, которые приведут к нужному событию. Это число сочетаний из  по
3. Перемножить количества из п. 1 и п. 2.

Запишем в виде общей формулы:
 

ИНДЕКС ПОИСКПОЗ с несколькими условиями в нескольких строках и столбцах

В этом примере показано, как выполнять поиск, проверяя два или более критерия в строках и столбцах. На самом деле это более сложный случай так называемого «матричного поиска» или «двустороннего поиска» с более чем одной строкой заголовка.

Вот общая формула ИНДЕКС ПОИСКПОЗ с несколькими критериями в строках и столбцах:

где:

Массив таблицы — область для поиска, т. е. все значения таблицы, кроме заголовков столбцов и строк.

Значение_поиска — то, что вы ищете по вертикали в столбце.

Столбец_поиска — диапазон столбцов для поиска, обычно это заголовки строк.

Значение_поиска1, значение_поиска2, … — то, что вы ищете по горизонтали в строках.

Строка_поиска1, строка_поиска2, … — диапазоны строк для поиска, обычно это заголовки столбцов.

Важное замечание! Чтобы формула работала корректно, ее нужно вводить как формулу массива  при помощи комбинации. Это разновидность классической формулы двустороннего поиска в массиве, которая ищет значение на пересечении определенной строки и столбца. Разница в том, что вы объединяете несколько значений и диапазонов поиска для оценки нескольких заголовков столбцов. Чтобы лучше понять логику ее работы, рассмотрим небольшой пример

Это разновидность классической формулы двустороннего поиска в массиве, которая ищет значение на пересечении определенной строки и столбца. Разница в том, что вы объединяете несколько значений и диапазонов поиска для оценки нескольких заголовков столбцов. Чтобы лучше понять логику ее работы, рассмотрим небольшой пример.

В приведенной ниже таблице мы будем искать значение на основе заголовков строк (элементы) и заголовков двух столбцов (регионы и поставщики). То есть, ищем по одному условию по строкам и по двум условиям – по столбцам. Чтобы упростить построение формулы, давайте сначала определим все критерии и диапазоны:

• Массив_таблицы — B3:E4
• Значение_поиска  — H1
• Столбец_поиска  (заголовки строк: товары) — A3:A5
• Значение_поиска1  (целевой регион) — H2
• Значение_поиска 2 (целевой продавец) — H3
• Строка_поиска1 (заголовки столбцов 1: регионы) — B1:E1
• Строка_поиска2 (заголовки столбцов 2: продавцы) — B2:E2

А теперь подставьте аргументы в общую формулу, описанную выше, и вы получите такой результат:

Не забудьте завершить формулу, нажав комбинацию клавиш , после чего поиск по матрице с несколькими условиями будет выполнен успешно:

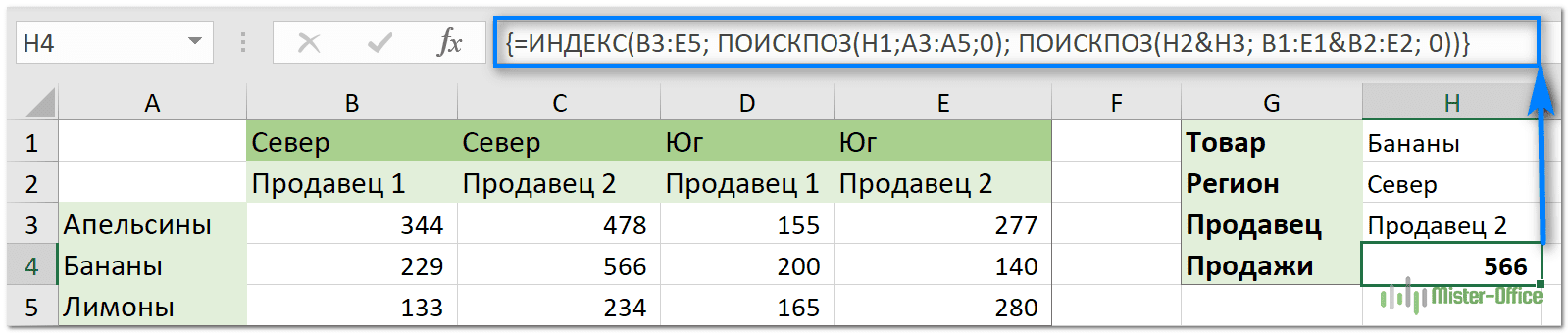
Пошагово рассмотрим, как работает эта формула.

Поскольку мы ищем и по вертикали, и по горизонтали, то нужно указать номера строк и столбцов для функции ИНДЕКС (массив, номер_строки, номер_столбца).

Шаг 1.

Номер_строки предоставляется функцией ПОИСКПОЗ(H1;A3:A5;0), которая сравнивает целевой элемент (бананы) в H1 с заголовками строк в A3:A5. 

ПОИСКПОЗ(«Бананы»;{«Апельсины»:»Бананы»:»Лимоны»};0)

Это дает результат 2, потому что «Бананы» — это второй элемент в указанном списке.

Шаг 2.

Номер_столбца вычисляется путем объединения двух значений поиска и двух массивов поиска: ПОИСКПОЗ(H2&H3; B1:E1&B2:E2; 0)

Необходимым условием является то, что значения поиска должны точно соответствовать заголовкам столбцов и быть объединены в том же порядке. Чтобы проследить процесс поиска, выберите первые два аргумента в формуле ПОИСКПОЗ, затем нажмите F9, и вы увидите, что оценивает каждый аргумент:

ПОИСКПОЗ(«СеверПродавец 2»; {«СеверПродавец 1″;»СеверПродавец 2″;»ЮгПродавец 1″;»ЮгПродавец 2»}; 0)

Поскольку « СеверПродавец 2» является вторым элементом в массиве, функция возвращает 2.

Шаг 3.

После этого наша длинная двумерная формула ИНДЕКС ПОИСКПОЗ превращается в такую простую:

=ИНДЕКС(B3:E5; 2; 2)

Шаг 4.

Она возвращает значение на пересечении 2-й строки и 2-го столбца в диапазоне B3:E5, что является значением в ячейке C4.

Вот как формула ИНДЕКС ПОИСКПОЗ помогает выполнить поиск по нескольким условиям в Excel. Я благодарю вас за чтение и надеюсь вновь увидеть вас в нашем блоге.

Формула сложных процентов в математике

Откуда берется эта формула расчета сложных процентов и как вообще все это работает, я подробно объяснял на предыдущем видеоуроке, поэтому если вы его не смотрели, очень рекомендую посмотреть. Однако из того же самого видеоурока возникла куча вопросов и, в частности, разбор самой сложной задачи мы оставили на потом. Именно этим мы сегодня и займемся.

Прежде чем решать эту задачу, давайте запишем нашу классическую формулу расчета сложных процентов, а именно:

\

Где $C$ — общая сумма кредита, $x$ — процент, $P$ — ежемесячный платеж, $n$ — срок, на который берется кредит.

Эту формулу мы выводили на одном из предыдущих видеоуроков, ее можно без всяких сомнений использовать на настоящем экзамене, при этом предварительно обосновав примерно так же, как это сделано в предыдущем видеоуроке.

Разбор 11 задания ОГЭ по информатике

Решение задания 11.1: Демонстрационный вариант ОГЭ 2022 г

В одном из произведений А.П. Чехова, текст которого приведён в подкаталоге каталога Проза, героиня произносит такую фразу: «Сегодня я в мерехлюндии, невесело мне, и ты не слушай меня».С помощью поисковых средств операционной системы и текстового редактора или браузера выясните имя этой героини.

Решение: 

• Поиск следует начать с каталога Проза. Для этого следует открыть папку Документы или Этот компьютер (или подобные названия в зависимости от операционной системы).
• Если не известно заранее расположение каталога, то ввести название каталога в строке поиска открытого окна:

Открыть найденный каталог. После чего в данном каталоге найти подкаталог с названием Чехов и открыть его.

В каталоге расположены файлы разного типа и с разными названиями. Рассмотрим варианты поиска в различного типа файлах.В файле или (Microsoft word):

Откройте файл и нажмите сочетание клавиш или в меню Главная выберите пункт Найти:
В строке поиска введите искомую фразу и чаще заменяя букву на . В нашем случае буква отсутствует.
Щелкните Найти. Если фраза найдена, то по контексту найдите главную героиню (если сюжет не известен, то лучше смотреть ближе к концу текста).

В файле (Блокнот):

Откройте файл и нажмите сочетание клавиш или в меню Правка выберите пункт Найти.

Повторите такие же действия поиска искомого слова, как и для предыдущего типа файла.

В файле (браузер):

Откройте файл и нажмите сочетание клавиш .

В различных браузерах отобразится разное поле для поиска. Повторите такие же действия поиска искомого слова, как и для предыдущего типа файла.

Ответ: Маша (Три сестры)

Решение задания 11.2: Демонстрационный вариант ОГЭ 2021 г

В одном из произведений И.С. Тургенева, текст которого приведён в подкаталоге Тургенев каталога DEMO-12, присутствует эпизод, происходящий на речке Гнилотёрке.С помощью поисковых средств операционной системы и текстового редактора выясните фамилию главного героя этого произведения.

Решение: 

• Поиск следует начать с каталога DEMO-12. Для этого следует открыть папку Документы или Этот компьютер (или подобные названия в зависимости от операционной системы).
• Если не известно заранее расположение каталога, то ввести название каталога в строке поиска открытого окна:

Открыть найденный каталог. После чего в данном каталоге найти подкаталог с названием Тургенев и открыть его.

В каталоге расположены файлы разного типа и с разными названиями. Рассмотрим варианты поиска в различного типа файлах.В файле или (Microsoft word):

Откройте файл и нажмите сочетание клавиш или в меню Главная выберите пункт Найти:
В строке поиска введите искомое слово без окончания и чаще заменяя букву на . Т.е. в нашем случае ««
Щелкните Найти. Если слово найдено, то по контексту найдите главного героя (если сюжет не известен, то лучше смотреть ближе к концу текста).

В файле (Блокнот):

Откройте файл и нажмите сочетание клавиш или в меню Правка выберите пункт Найти.

Повторите такие же действия поиска искомого слова, как и для предыдущего типа файла.

В файле (браузер):

Откройте файл и нажмите сочетание клавиш .

В различных браузерах отобразится разное поле для поиска. Повторите такие же действия поиска искомого слова, как и для предыдущего типа файла.

Ответ: ОВСЯНИКОВ (Записки охотника)

Ответы на вопрос

Внимание! Ответы на вопросы дают живые люди. Они могут содержать ошибочную информацию, заблуждения, а также ответы могут быть сгенерированы нейросетями

Будьте внимательны. Если вы уверены, что ответ неверный, нажмите кнопку «Пожаловаться» под ответом.

Отвечает Назаров Олег.

В кодировке Unicode один символ занимает 2 байта => из формулы V=k*i выражаем k;V=128 КБайт. Переведём в байты: 1024*128 Байтk=V/i => 128*1024/2=65536Ответ: 65536

Отвечает Кривко Сергей.

Информационный объем текста книги, набранной на компьютере с использованием кодировки Unicode 128 килобайт, составляет 128 килобайт.

Однако, для определения количества символов в тексте книги, нам необходимо знать, какой именно текст содержится в книге. Без этой информации, невозможно точно определить количество символов в тексте.

Если у вас есть конкретный текст, вы можете использовать различные инструменты для подсчета символов, такие как текстовые редакторы или онлайн-счетчики символов. Эти инструменты могут точно подсчитать количество символов в тексте книги.

Надеюсь, это помогло! Если у вас есть еще вопросы, не стесняйтесь задавать.

Последние заданные вопросы в категории Информатика

Информатика 15.12.2023 10:42 113 Двалишвили Майя

C++ Нехай с=10. Чому дорівнює х після виконання команди x=(c==3) ? 2+c : c-2; Виберіть одну

Ответов: 1

Информатика 15.12.2023 10:03 125 Абикенова Ерке

Сколько раз такимичи чуть не умер?

Ответов: 2

Информатика 15.12.2023 09:39 95 Шагас Артем

Придумать базу данных которая содержит 5 полей и 4 записи типы полей должны быть разными​

Ответов: 2

Информатика 15.12.2023 08:01 35 Тарасов Влад

Write the following sums in sigma notation (i.e. using the symbol P): 7+12+17+22+27+32;

Ответов: 2

Информатика 15.12.2023 06:46 44 Прокопов Миша

Даны числа a и b найти сумму чисел между ними python​

Ответов: 2

Информатика 15.12.2023 02:07 28 Власова Лена

10. Які параметри накреслення символів в даному реченні? Навчаючи інших, також вчися. а)

Ответов: 1

Информатика 15.12.2023 00:44 22 Полякова Наталья

До основних функцій текстового процесора належать срочно​

Ответов: 2

Информатика 14.12.2023 19:52 43 Валеев Радмир

Дано целое число N (>0). Найти значение выражения 1.1 — 1.2 + 1.3… (N слагаемых, знаки

Ответов: 1

Информатика 14.12.2023 17:29 23 Осипова София

Встановіть відповідність між ТЕРМІНОМ «Ключові слова» ТА ЙОГО ПРИЗНАЧЕННЯМ 1 Слова, що вводяться

Ответов: 1

Информатика 14.12.2023 16:18 32 Стрельников Андрей

Найдите единицу измерения информацы

Ответов: 2

Полезные советы при решении задач с использованием формулы сложных процентов

Самое главное в это задаче — это понять, чем оценки отличаются от округления. Мы берем две цифры после запятой, отсекаем все, что идет после них, и записываем эти числа слева. Очевидно, что поскольку дальше идут какие-то цифры в настоящем числе, это число будет то, что мы получили слева (см. таблицу). Эти числа, которые находятся слева, и называются меньшими оценками. Затем к ним мы в самом последнем разряде (к последней цифре) прибавляем «единицу», и получаем число, на единицу большее в конце, например, было $1,06$ стало $1,07$ и т.д. Это будут верхние оценки. И далее, что бы мы не делали, какую бы степень и номер месяца не считали, все равно истинное значение нашей величины будет заключено между степенями верхней и нижней оценок.

Но есть одна проблема: в определенный момент мы получаем, что и число, и искомая величина лежат в одних и тех же пределах. Пределы получены, разумеется, при вычислении степеней оценок. В нашей ситуации такая проблема возникла в вычислениях значения для пятого месяца: левая оценка дала нам $1,1554$, а правая — $1,177$. Между этими двумя числами лежит как искомая величина, которую мы не знаем, так и наше искомое значение, т.е. ${{1,03}^{n}}$. Выход из такой ситуации напрашивается сам собой: если нам не хватает точности, то необходимо просто увеличить точность исходных оценок, т.е. после запятой мы берем не две, а три цифры. Но поскольку нас интересуют, прежде всего, верхние оценки, мы увеличим каждое из этих чисел на единицу в разряде, запишем и перемножим. В результате мы получим следующее: новая верхняя оценка для нашего числа, для пятого месяца, будет лежать между $1,1554$ и $1,159673$.

На самом деле, пятый месяц даст коэффициент, который будет находиться в вышеуказанном диапазоне, что явно меньше, чем искомая величина $1,174647…$ На первый взгляд может показаться, что сложность и объем всех этих вычислений будет существенно больше, чем если бы мы просто возвели числа в степень квадрат, куб и т.д. На самом деле это не так. Уже на третьей и четвертой степенях возникают большие числа, а до пятого и шестого месяца вы просто не дойдете.

Как определить кандидата в ответ, исходя из условия задачи

В качестве заключительного аккорда сегодняшнего видеоурока я хотел бы вам рассказать еще один довольно хитрый инструмент, который позволит еще с первого взгляда на задачу уже примерно оценить, какой месяц предстоит считать и какой месяц, скорее всего, является кандидатом в ответ.

Давайте посмотрим на исходную формулу. Всего объем кредит, который предстоит выплатить, составляет 1,1 млн. при этом ежемесячно нужно выплачивать по 220 тыс. рублей. Давайте разделим общий размер задолженности на ежемесячный платеж. В этом случае мы получим количество месяцев, которые необходимо будет потратить на выплату кредита, если бы на нас не начислялись проценты. Однако сами по себе проценты невелики — в нашем случае всего 3% в месяц. Это значит, что вряд ли накопится задолженность еще больше, чем на один месяц и, следовательно, нужно прибавить к полученной величине еще единицу, и мы получим наиболее вероятный кандидат на ответ.

В нашем случае, если 1,1млн. разделить на 220 тыс., то мы получим пять месяцев, но без учета начисленных процентов. Соответственно, еще один месяц потребуется на то, чтобы погасить проценты. И мы получим тот же самый ответ.

Однако хочу вас предупредить, что ни в коем случае нельзя использовать этот прием как единственно возможное обоснование того ответа, который у вас получается в задаче! Потому что мы решаем одну из самых сложных задач ЕГЭ: там требуется привести не только ответ, но и все подробные выкладки и обоснования. Такой прием — это лишь подсказка для нас самих, для того, чтобы понимать, какие именно месяцы, какие именно степени считать. Дальнейшим шагом нужно доказать, что, например, число, равное пяти месяцам, нас не устраивает, а шести месяцев точно устраивает. Каким образом можно это сделать. Например, с помощью числовой прямой, более точных вычислений, метода оценок или как вам будет удобнее. В любом случае, мы с учениками недавно убедились, что эта подсказка существенно облегчает выкладки и хотя бы дает представление о том, каким должен быть ответ.

Тренируйтесь, решайте задачи, оттачивайте навык с вычислением верхних и нижних оценок. Это далеко не последний урок на решение задач с экономическим содержанием, поскольку самих задач стало довольно много, и их условия стали более разнообразные. Поэтому оставайтесь с нами!

1. Задачи на кредит с плавающим платежом
2. Производительность труда в задаче 17 из ЕГЭ по математике: сложные случаи. Нет, это не текстовые задачи.:)
3. Тест к уроку «Что такое логарифм» (средний)
4. Комментарий к пробному ЕГЭ от 7 декабря
5. Опасные ошибки в задачах на площади
6. Задача B4: экономика

Самая сложная задача про кредиты из ЕГЭ

Сегодня мы разберем то, о чем я обещал поговорить еще в прошлом учебном году, когда мы впервые познакомились с задачами с экономическим содержанием из ЕГЭ по математике. Вообще, с момента появления этой задачи в Едином государственном экзамене прошло довольно много времени, и с тех пор такие задачи стали более разнообразными, чем изначально, однако самая сложная и часто встречающаяся задача осталась неизменной. Именно о ней мы сегодня и поговорим. А точнее, речь пойдет о самом сложном варианте этой задачи — о задаче на выплаты и кредиты, когда работает универсальная формула сложных процентов, выведенная в предыдущем видеоуроке, однако неизвестно в этот раз не кредит и не платеж, а именно время, на который взят этот самый кредит.

Вероятность попадания в конечный интервал

Функция распределения помогает решить ещё и такую задачу: найти вероятность, что случайная величина попадёт в конечный интервал.
 
Вернёмся к примеру со временем реакции беспилотного автомобиля на препятствие. Задача может быть такой. Время реакции распределено нормально:  Нужно найти вероятность, что автомобиль среагирует на препятствие за время от  до  миллисекунд, то есть

 
Чтобы рассчитать вероятность, что случайная величина попадёт в интервал, нужно:

1. Найти кумулятивную вероятность меньшего значения.
2. Найти кумулятивную вероятность большего значения.
3. Вычесть из большей вероятности меньшую. «Хвост» распределения левее меньшего значения сократится и останется только интервал между значениями.

Выводы

Итак, в этом уроке вы узнали главное о распределении Пуассона:

• Задаётся одним параметром , который интерпретируют как интенсивность процесса: сколько раз событие происходит за конкретный период;
• Определено для всех неотрицательных целых чисел, каждое из которых интерпретируют как количество произошедших событий за этот период;
• Если случайная величина  распределена по Пуассону с параметром , то есть , вероятность того, что за период произойдёт  событий, рассчитывают по формуле
• Параметр  можно пересчитывать для других промежутков времени пропорционально соотношению длительности нового и старого периодов.
• В модуле есть метод для получения вероятностей распределения Пуассона и метод для получения значений его функции распределения.