Кодирование вещественных чисел
Несколько иной способ применяется для представления в памяти
персонального компьютера действительных чисел. Рассмотрим представление
величин с плавающей точкой.
Любое действительное число можно записать в стандартном виде M × 10p,
где 1 £ M p целое. Например, 120100000 = 1,201 × 108. Поскольку
каждая позиция десятичного числа отличается от соседней на степень числа
10, умножение на 10 эквивалентно сдвигу десятичной запятой на одну позицию
вправо. Аналогично деление на 10 сдвигает десятичную запятую на позицию
влево. Поэтому приведенный выше пример можно продолжить: 120100000 = 1,201 × 108 = 0,1201 × 109 = 12,01 × 107. Десятичная запятая «плавает» в числе
и больше не помечает абсолютное место между целой и дробной частями.
В приведенной выше записи M называют мантиссой числа, а p его
порядком. Для того чтобы сохранить максимальную точность, вычислительные
машины почти всегда хранят мантиссу в нормализованном виде, что означает,
что мантисса в данном случае есть число, лежащее между 1(10) и 2(10) (1 £ M
Современный персональный компьютер
позволяет работать со следующими действительными типами (диапазон значений
указан по абсолютной величине; в некоторых случаях перечень типов данных может быть расширен):
| Тип | Диапазон | Мантисса | Байты |
|---|---|---|---|
| Real | 2,9×10-39..1,7×1038 | 11-12 | 6 |
| Single | 1,5×10-45..3,4×1038 | 7-8 | 4 |
| Double | 5,0×10-324..1,7×10308 | 15-16 | 8 |
| Extended | 3,4×10-4932..1,1×104932 | 19-20 | 10 |
Покажем преобразование действительного числа для представления его в
памяти ЭВМ на примере величины типа Double.
Как видно из таблицы, величина это типа занимает в памяти 8 байт. На
рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):
| S | Смещенный порядок | Мантисса |
| 63 | 62..52 | 51..0 |
Можно заметить, что старший бит, отведенный под мантиссу, имеет номер
51, т.е. мантисса занимает младшие 52 бита. Черта указывает здесь на
положение двоичной запятой. Перед запятой должен стоять бит целой части
мантиссы, но поскольку она всегда равна 1, здесь данный бит не требуется и
соответствующий разряд отсутствует в памяти (но он подразумевается).
Значение порядка хранится здесь не как целое число, представленное в
дополнительном коде. Для упрощения вычислений и сравнения действительных
чисел значение порядка в ЭВМ хранится в виде смещенного числа, т.е. к
настоящему значению порядка перед записью его в память прибавляется
смещение. Смещение выбирается так, чтобы минимальному значению порядка
соответствовал нуль. Например, для типа Double порядок занимает 11 бит и
имеет диапазон от 2-1023 до 21023, поэтому смещение равно 1023(10) =
1111111111(2). Наконец, бит с номером 63 указывает на знак числа.
Таким образом, из вышесказанного вытекает следующий алгоритм для
получения представления действительного числа в памяти ЭВМ:
- перевести модуль данного числа в двоичную систему счисления;
- нормализовать двоичное число, т.е. записать в виде M × 2p, где M
мантисса (ее целая часть равна 1(2)) и p порядок, записанный в
десятичной системе счисления; - прибавить к порядку смещение и перевести смещенный порядок в двоичную
систему счисления; - учитывая знак заданного числа (0 положительное; 1 отрицательное),
выписать его представление в памяти ЭВМ.
Пример. Запишем код числа -312,3125.
- Двоичная запись модуля этого числа имеет вид 100111000,0101.
- Имеем 100111000,0101 =
1,001110000101 × 28. - Получаем смещенный порядок 8 + 1023 = 1031. Далее имеем
1031(10) = 10000000111(2). - Окончательно
1 10000000111 0011100001010000000000000000000000000000000000000000 63 62..52 51..0
Очевидно, что более компактно полученный код стоит записать следующим
образом: C073850000000000(16).
Другой пример иллюстрирует обратный переход от кода действительного
числа к самому числу.
Пример. Пусть дан код 3FEC600000000000(16) или
| 01111111110 | 1100011000000000000000000000000000000000000000000000 | |
| 63 | 62..52 | 51..0 |
- Прежде всего замечаем, что это код положительного числа, поскольку в
разряде с номером 63 записан нуль. Получим порядок этого числа:
01111111110(2) = 1022(10); 1022 — 1023 = -1. - Число имеет вид 1,1100011 × 2-1 или
0,11100011. - Переводом в десятичную систему счисления получаем 0,88671875.
Можно проверить себя:
Онлайн преобразователь для IEEE 754 чисел с двойной точностью
См. также стандарт IEEE 754
Контрольная работа по предсталению информации в памяти ЭВМ
А.П. Шестаков, 1999-2009
Сайт создан в системе uCoz
Вопрос посетителя
Выполните подстановку операции так, чтобы равенство (1 _ 1) OR NOT (1 _ 0) = 0 оказалось верным
(*ответ*) исключающее ИЛИ (XOR)
логическое И (AND)
логическое ИЛИ (OR)
отрицание (NOT)
Высказыванию «А не является max (A,B,C) и не является min (A,B,C)» соответствует логическое выражение
(*ответ*) (А С) или (А В)
(А > В) или (А С)
(А
(А B) и (А C)
Данные входят в состав команд компьютера в виде
(*ответ*) операндов
инструкций
предикатов
функций
Два младших разряда двоичной записи числа, кратного 4, имеют вид…
(*ответ*) 00
01
10
22
Десятичному числу 3710 соответствует двоичное число
(*ответ*) 100101
111011
101110
101010
Десятичному числу 3710 соответствует двоичное число
(*ответ*) 100101
111011
101110
101010
Для запоминания 1 байта информации достаточно _ триггера(ов)
(*ответ*) 8
2
16
1
Для информационной техники предпочтительнее _ вид сигнала
(*ответ*) цифровой
синхронизированный
зашумленный
непрерывный
Для информационной техники предпочтительнее _ вид сигнала
(*ответ*) цифровой
синхронизированный
зашумленный
непрерывный
Для кодирования цвета одной точки, воспроизводимой на экране сотового телефона, используется 3 бита. Сотовый телефон имеет разрешение экрана 96*68 точек. Минимальный объем видеопамяти равен
(*ответ*) 2448 байт
6528 байт
19584 байт
52224 байт
Для обработки в оперативной памяти компьютера числа преобразуются в
(*ответ*) числовые коды в двоичной форме
символы латинского алфавита
числовые коды в восьмеричной форме
графические образы
Для хранения в оперативной памяти символы преобразуются в
(*ответ*) числовые коды в двоичной системе счисления
графические образы
числовые коды в шестнадцатиричной форме
числовые коды в десятичной системе счисления
Представление целых чисел в дополнительном коде
Другой способ представления целых чисел дополнительный код. Диапазон значений величин зависит от количества бит памяти, отведенных для их хранения. Например, величины типа Integer (все названия типов данных здесь и ниже представлены в том виде, в каком они приняты в языке программирования Turbo Pascal. В других языках такие типы данных тоже есть, но могут иметь другие названия) лежат в диапазоне от -32768 (-215) до 32767 (215 — 1) и для их хранения отводится 2 байта (16 бит); типа LongInt в диапазоне от -231 до 231 — 1 и размещаются в 4 байтах (32 бита); типа Word в диапазоне от 0 до 65535 (216 — 1) (используется 2 байта) и т.д.
Как видно из примеров, данные могут быть интерпретированы как числа со знаком, так и без знака. В случае представления величины со знаком самый левый (старший) разряд указывает на положительное число, если содержит нуль, и на отрицательное, если единицу.
Вообще, разряды нумеруются справа налево, начиная с 0. Ниже показана нумерация бит в двухбайтовом машинном слове.
| 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | |
Дополнительный код положительного числа совпадает с его прямым кодом.
Прямой код целого числа может быть получен следующим образом: число
переводится в двоичную систему счисления, а затем его двоичную запись
слева дополняют таким количеством незначащих нулей, сколько требует тип
данных, к которому принадлежит число.
Например, если число 37(10) =
100101(2) объявлено величиной типа Integer (шестнадцатибитовое со знаком), то его прямым кодом будет
0000000000100101, а если величиной типа LongInt (тридцатидвухбитовое со знаком), то его прямой код будет
00000000000000000000000000100101. Для более компактной записи чаще
используют шестнадцатеричное представление кода. Полученные коды можно переписать
соответственно как 0025(16) и 00000025(16).
Дополнительный код целого отрицательного числа может быть получен по
следующему алгоритму:
- записать прямой код модуля числа;
- инвертировать его (заменить единицы нулями, нули единицами);
- прибавить к инверсному коду единицу.
Например, запишем дополнительный код числа -37, интерпретируя его как
величину типа LongInt (тридцатидвухбитовое со знаком):
- прямой код числа 37 есть 00000000000000000000000000100101;
- инверсный код 11111111111111111111111111011010;
- дополнительный код 11111111111111111111111111011011 или
FFFFFFDB(16).
При получении числа по его дополнительному коду прежде всего необходимо
определить его знак. Если число окажется положительным, то просто
перевести его код в десятичную систему счисления. В случае отрицательного
числа необходимо выполнить следующий алгоритм:
- вычесть из кода числа 1;
- инвертировать код;
- перевести в десятичную систему счисления. Полученное число записать со
знаком минус.
Примеры. Запишем числа, соответствующие дополнительным
кодам:
- 0000000000010111. Поскольку в старшем разряде записан нуль, то
результат будет положительным. Это код числа 23. - 1111111111000000. Здесь записан код отрицательного числа. Исполняем алгоритм:
1) 1111111111000000(2) — 1(2) = 1111111110111111(2); 2) 0000000001000000;
3) 1000000(2) = 64(10).
Ответ: -64.
§ 2.1. Кодирование текстовой информации
Содержание урока
Кодирование текстовой информации
Кодирование текстовой информации
Двоичное кодирование текстовой информации в компьютере.
Информация, выраженная с помощью естественных и формальных языков в письменной форме, обычно называется текстовой информацией.
Для представления текстовой информации (прописные и строчные буквы русского и латинского алфавитов, цифры, знаки и математические символы) достаточно 256 различных знаков. По формуле (1.1) можно вычислить, какое количество информации необходимо, чтобы закодировать каждый знак:
N = 2I ⇒ 256 = 2I ⇒ 28 = 2I ⇒ I = 8 битов.
Для обработки текстовой информации в компьютере необходимо представить ее в двоичной знаковой системе. Для кодирования каждого знака требуется количество информации, равное 8 битам, т. е. длина двоичного кода знака составляет восемь двоичных знаков. Каждому знаку необходимо поставить в соответствие уникальный двоичный код в интервале от 00000000 до 11111111 (в десятичном коде от 0 до 255) (табл. 2.1).
Человек различает знаки по их начертанию, а компьютер — по их двоичным кодам. При вводе в компьютер текстовой информации происходит ее двоичное кодирование. Пользователь нажимает на клавиатуре клавишу со знаком, и в компьютер поступает определенная последовательность из восьми электрических импульсов (двоичный код знака). Код знака хранится в оперативной памяти компьютера, где занимает одну ячейку (размером 1 байт).
В процессе вывода знака на экран компьютера производится обратное кодирование, т. е. преобразование двоичного кода знака в его изображение.
Таблица 2.1. Кодировки знаков>
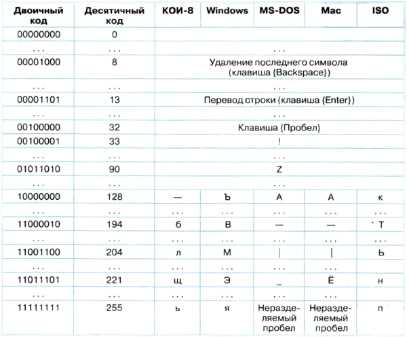
Различные кодировки знаков. Присвоение знаку конкретного двоичного кода — это вопрос соглашения, которое фиксируется в кодовой таблице. Первые 33 кода в кодовой таблице (десятичные коды с 0 по 32) соответствуют не знакам, а операциям (перевод строки, ввод пробела и т. д.).
Десятичные коды с 33 по 127 являются интернациональными и соответствуют знакам латинского алфавита, цифрам, знакам арифметических операций и знакам препинания.
Десятичные коды с 128 по 255 являются национальными, т. е. в различных национальных кодировках одному и тому же коду соответствуют разные знаки. К сожалению, в настоящее время существуют пять различных кодовых таблиц для русских букв (Windows, MS-DOS, КОИ-8, Mac, ISO), поэтому тексты, созданные в одной кодировке, не будут правильно отображаться в другой.
В последние годы широкое распространение получил новый международный стандарт кодирования текстовых символов Unicode, который отводит на каждый символ 2 байта (16 битов). По формуле (1.1) определим количество символов, которые можно закодировать:
N = 2I = 216 = 65 536.
Такого количества символов оказалось достаточно, чтобы закодировать не только русский и латинский алфавиты, цифры, знаки и математические символы, но и греческий, арабский, иврит и другие алфавиты.
Итак, в настоящее время имеется шесть различных кодировок для букв русского алфавита, в которых один и тот же знак имеет различные коды (табл. 2.2). К счастью, в большинстве случаев пользователь не должен заботиться о перекодировках текстовых документов, так как это делают специальные программы-конверторы, встроенные в операционную систему и приложения.
Таблица 2.2. Десятичные коды некоторых знаков в различных кодировках
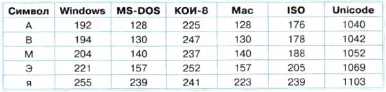
Например, в кодировке Windows последовательность числовых кодов 221 194 204 образует слово «ЭВМ» (см. табл. 2.2), тогда как в других кодировках это будет бессмысленный набор символов.
Контрольные вопросы
1. Почему при кодировании текстовой информации в компьютере в большинстве кодировок используется 256 различных символов, хотя русский алфавит включает только 33 буквы?
2. С какой целью ввели кодировку Unicode, которая позволяет закодировать 65 536 различных символов? Подготовьте сообщение.
Задания для самостоятельного выполнения
2.1. Задание с кратким ответом. В текстовом режиме экран монитора компьютера обычно разбивается на 25 строк по 80 символов в строке. Определите объем текстовой информации, занимающей весь экран монитора, в кодировке Unicode.
2.2. Задание с развернутым ответом. Пользователь компьютера, хорошо владеющий навыками ввода информации с клавиатуры, может вводить в минуту 100 знаков. Какое количество информации может ввести пользователь в компьютер за одну минуту в кодировке Windows? В кодировке Unicode?
Cкачать материалы урока





















![[клякс@.net][информатика и икт в школе. компьютер на уроках.][[экзамен по информатике][билет №4][представление и кодирование информации]]](http://portalcomp.ru/wp-content/uploads/c/5/e/c5edf4f36bf4e1cfe52457ea280384e6.jpeg)









