Системы счисления, используемые в компьютере

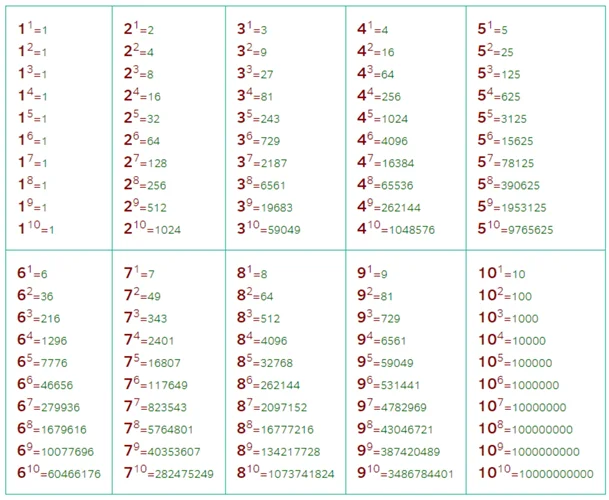
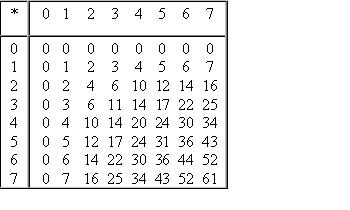
Что такое системы счисления

Системы счисления, производные от двоичной

Итак, в электронно-вычислительных машинах (компьютерах) вся информация хранится и обрабатывается в бинарном формате. Каждому разряду в двоичном числе соответствует 0 или 1. Такой разряд называется битом. Например, с помощью двух бит можно записать числа

Замечание 2

Предпринимались небезуспешные попытки создавать компьютеры на основе троичной логики, но такие машины не обрели особой популярности.

Спецификой обработки двоичных данных является то, что в регистры процессора они попадают порциями определенного размера: по 4, 8, 16, 32, 64 разряда за одну простейшую операцию (такт). Сколько именно разрядов обрабатывает процессор за 1 такт, зависит от его архитектуры. Большинство современных процессоров работают с 64-разрядными данными, а в 1970-х компания Intel начинала свою деятельность с 4-разрядных процессоров, которым быстро пришли на смену 8-разрядные. Именно тогда 8-битное число и получило большое распространение в программировании. За ним даже закрепилось особое название — байт. 1 байт содержит — 8 бит информации. Максимальное натуральное число, которое можно закодировать одним байтом — 255. С учетом числа 0, которое, конечно же, можно выразить с помощью байта, он может принимать 256 различных состояний.

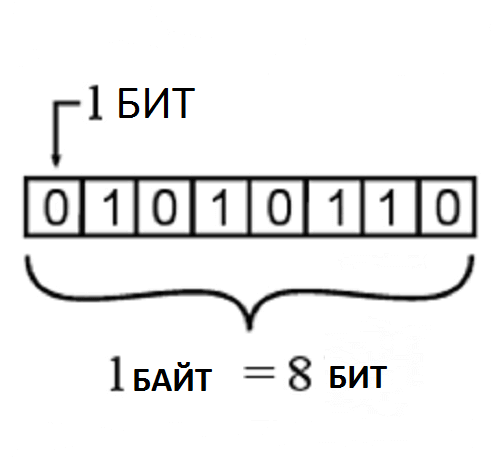Рисунок 3. Бит и байт. Автор24 — интернет-биржа студенческих работ

Со временем программисты пришли к выводу, что байты удобно записывать в виде 2-х шестнадцатеричных знаков. В шестнадцатеричном счислении, помимо обычных арабских цифр содержатся дополнительные символы:

Чтобы записать число от 0 до 255 в 16-ричной кодировке, нужно задействовать два таких символа (их иногда называют полубайтами, тетрадами, нибблами и даже гексадецитами). Признаком того, что число записано в такой форме являются символы в его начале

Помимо шестнадцатеричной в программировании иногда применяется восьмеричная система счисления.

Виды

Почему в ЭВМ используется двоичная система счисления

Почему использовалась в начале эры ЭВМ?

Ответ прост — на это повлияли законы физики и особенности развития аппаратного обеспечения. Вспомните, как выглядели первые ЭВМ – большие установки, которые занимали по площади размер, сопоставимый с теннисным кортом.

1. Простота технической реализации;Есть всего два состояния, а это значит, что можно подобрать большое количество физических процессов, для представления данных. Например, ток (подается или нет), магнитная дорожка (отрезок дорожки намагничен или нет).
2. Большая надежность;
3. Высокая помехоустойчивость.

Второй и третий плюс вытекают из первого. Да и в то время технологии были не настолько развиты, чтобы можно было предложить более практичное решение. Революция произошла в конце пятидесятых, начале шестидесятых годов, когда были выпущены первые кремниевые транзисторы.

Почему мы пользуемся ей сейчас?

Сейчас будет сложно, так что приготовьтесь. Процессоры всех современных компьютеров и других цифровых устройств работают на основе схемотехнических элементов, которые называются транзисторы.

Итак, что это такое? Если говорить просто, то это элемент, который позволяет управлять электрическим током. Рассмотрим принцип его действия.

Элемент состоит из трех частей:

1. Полупроводниковой подложки;
2. Области P-типа:
3. Области N-типа.

Однако грош цена была бы этому изобретению – если с помощью транзистора можно было выводить только нуль и единицу. Почему? Какой смысл от букв и цифр, если мы не можем с ними выполнять различные операции.

4.10. Как производятся арифметические операции в позиционных системах счисления?

Рассмотрим основные арифметические операции: сложение, вычитание,
умножение и деление. Правила выполнения этих операций в десятичной системе
хорошо известны — это сложение, вычитание, умножение столбиком  
и  деление углом. Эти правила применимы и ко всем другим позиционным
системам счисления. Только таблицами сложения и умножения надо пользоваться
особыми для каждой системы.

С л о ж е н и е

Таблицы сложения легко составить, используя Правило Счета.
 

Сложение в двоичной системе

Сложение в восьмеричной системе

                
Сложение в шестнадцатиричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток,
то он переносится влево.
 
  Пример 1. Сложим числа 15 и 6 в
различных системах счисления.

     

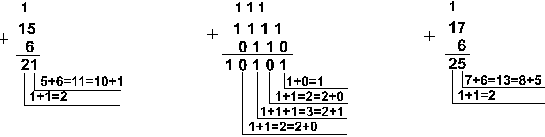
Шестнадцатеричная: F16+616

Ответ: 15+6 = 2110 = 101012 = 258 = 1516.  Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 2 = 16+4+1=21,  258 = 2. 81 + 5. 8 = 16 + 5 = 21,  1516 = 1. 161 + 5. 16 = 16+5 = 21.

  Пример 2. Сложим числа 15, 7 и 3.

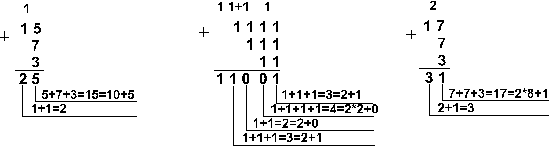
Шестнадцатеричная: F16+716+316

Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916.  Проверка: 110012 = 24 + 23 + 2 = 16+8+1=25, 318 = 3. 81 + 1. 8 = 24 + 1 = 25,  1916 = 1. 161 + 9. 16 = 16+9 = 25.

  Пример 3. Сложим числа 141,5 и
59,75.

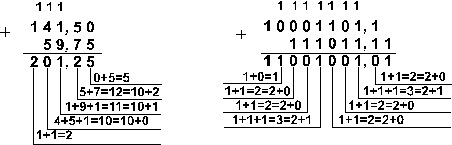
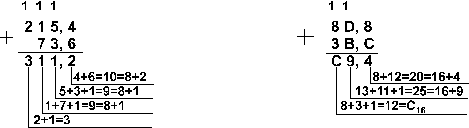
  Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ =
311,2₈ = C9,4₁₆Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,01₂ = 27 + 26 + 23 + 2
+ 2-2 = 201,25
311,2₈ = 3. 82 + 181 + 1. 8 + 2. 8-1 = 201,25
C9,4₁₆ = 12. 161 + 9. 16
+ 4. 16-1 = 201,25

В ы ч и т а н и е

Пример 4.Вычтем единицу из чисел 10₂, 10₈
и 10₁₆
     
     
 
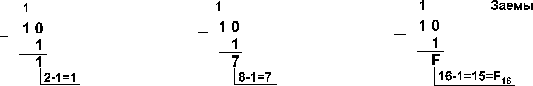
  Пример 5. Вычтем единицу из чисел
100₂, 100₈ и 100₁₆.
     
     
 
  Пример 6. Вычтем число 59,75 из
числа 201,25.

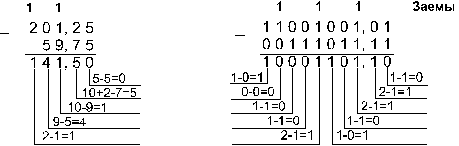
  Ответ: 201,25₁₀ — 59,75₁₀ = 141,5₁₀ =
10001101,1₂ = 215,4₈ = 8D,8₁₆. Проверка. Преобразуем полученные разности к десятичному виду:
10001101,1₂ = 27 + 23 + 22 + 2
+ 2-1 = 141,5;
215,4₈ = 2. 82 + 1. 81
+ 5. 8 + 4. 8-1 =
141,5;
8D,8₁₆ = 8. 161 + D. 16
+ 8. 16-1 = 141,5.

У м н о ж е н и е

Выполняя умножение многозначных чисел в различных позиционных системах
счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но
при этом результаты перемножения и сложения однозначных чисел необходимо
заимствовать из соответствующих рассматриваемой системе таблиц умножения и
сложения.

Умножение в двоичной системе

Умножение в восьмеричной системе

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение
сводится лишь к сдвигам множимого и сложениям.
 
  Пример 7. Перемножим числа 5 и 6.

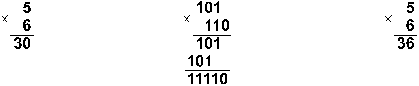Ответ: 5. 6 = 30₁₀ = 11110₂ =
36₈. Проверка. Преобразуем полученные произведения к десятичному виду:
11110₂ = 24 + 23 + 22 + 21
= 30;
36₈ = 381 + 68 = 30.
 
  Пример 8. Перемножим числа 115 и
51.

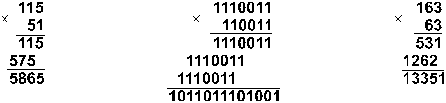Ответ: 115. 51 = 5865₁₀ = 1011011101001₂
= 13351₈. Проверка. Преобразуем полученные произведения к десятичному виду:
1011011101001₂ = 212 + 210 + 29 + 27
+ 26 + 25 + 23 + 2 = 5865;
13351₈ = 1. 84 + 3. 83
+ 3. 82 + 5. 81 + 1. 8 = 5865.

Д е л е н и е

Деление в любой позиционной системе счисления производится
по тем же правилам, как и деление углом в десятичной системе. В двоичной
системе деление выполняется особенно просто, ведь очередная цифра частного
может быть только нулем или единицей.
 
  Пример 9. Разделим число 30 на
число 6.

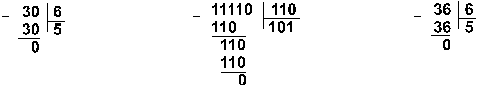Ответ: 30 : 6 = 5₁₀ = 101₂ = 5₈.
 
  Пример 10. Разделим число 5865 на
число 115.

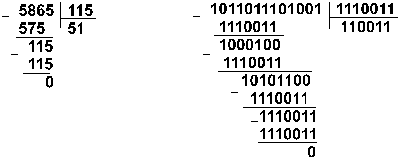
Восьмеричная: 13351₈ :163₈

Ответ: 5865 : 115 = 51₁₀ = 110011₂ = 63₈.
Проверка. Преобразуем полученные частные к десятичному виду:
110011₂ = 25 + 24 + 21 + 2
= 51; 63₈ = 6. 81 + 3. 8
= 51.
 
  Пример 11. Разделим число 35 на число
14.

Восьмеричная: 43₈ : 16₈

Ответ: 35 : 14 = 2,5₁₀ = 10,1₂ = 2,4₈. Проверка. Преобразуем полученные частные к десятичному виду:
10,1₂ = 21 + 2 -1 = 2,5;
2,4₈ = 2. 8 + 4. 8-1
= 2,5.
 
 

4.14. Как компьютер выполняет арифметические действия над нормализованными числами?

К началу выполнения арифметического действия операнды операции помещаются
в соответствующие регистры АЛУ.

При сложении и вычитании сначала производится подготовительная операция,
называемая выравниванием порядков.

В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.

В результате выравнивания порядков одноименные разряды чисел оказываются
расположенными в соответствующих разрядах обоих регистров, после чего
мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига
мантиссы результата влево. После каждого сдвига влево порядок результата
уменьшается на единицу.

Пример 1. Сложить двоичные нормализованные числа 0.10111 . 2-1
и 0.11011 . 210. Разность порядков слагаемых здесь равна трем, поэтому
перед сложением мантисса первого числа сдвигается на три разряда вправо:

Пример 2. Выполнить вычитание двоичных нормализованных чисел 0.10101 . 210
и 0.11101 . 21. Разность порядков уменьшаемого и вычитаемого здесь
равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на
один разряд вправо:

Результат получился не нормализованным, поэтому его мантисса
сдвигается влево на два разряда с соответствующим уменьшением порядка
на две единицы: 0.1101 . 2.

При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются.

Пример 3. Выполнить умножение двоичных нормализованных чисел:

(0.11101 . 2101) . (0.1001 . 211) = (0.11101 . 0.1001) .
2(101+11) = 0.100000101 . 21000.

При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется.

Пример 4. Выполнить деление двоичных нормализованных чисел:

0.1111 . 2100 : 0.101 . 211 = (0.1111 : 0.101)
. 2(100-11) = 1.1 . 21 = 0.11 . 210.

Использование представления чисел с плавающей точкой существенно
усложняет схему арифметико-логического устройства.

Недостатки двоичного кода

Сложность чтения. Записанная с помощью 0 и 1 информация нечитаема для человека, не обладающего специальными знаниями и обучения. Расшифровка двоичного кода на понятный язык может быть очень сложной и требует использования специальных методов и программ.

Высокая сложность программирования. Написание программы на двоичном коде невозможно без глубокого понимания и экспертизы в области низкоуровневого программирования. Это требует большого количества усилий и времени, особенно для составления длинных и сложных программ.

Ограниченная емкость. Двоичное представление требует больше символов для тех же данных по сравнению с другими системами кодирования. Это может привести к увеличению размера файла или затратам на дополнительное хранение.

Сложность визуализации. Двоичный код трудно визуализировать, особенно для больших наборов данных. Это может затруднять его отслеживание и анализ без использования специальных инструментов и программ.

Таким образом, двоичное кодирование информации остается на данный момент основным способом, используемым в вычислительных устройствах. На нем основана вся логическая архитектура смартфонов, планшетов, ПК, огромных суперкомпьютеров, бортовых вычислительных систем самолетов, космических аппаратов, кораблей и т. д. Тем не менее у него есть недостатки, которые ограничивают развитие компьютерной техники. Возможно, в связи с экспоненциальным ростом потребности в эффективной обработке информации в будущем бинарный код уступит место альтернативным способам кодировки.

Другие термины на «Д»

ДампДоменДрайверДедлайнДисперсияДекомпозиция
Все термины

Подсчет в двоичном формате

В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.

1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)

Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.

Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.

Распространенные системы счисления в информатике

Двоичная система счисления

Двоичная система счисления основана на использовании только двух цифр: 0 и 1. Это основная система счисления, используемая в компьютере для представления информации.

В двоичной системе счисления каждая цифра называется битом (от англ. binary digit). Бит может иметь два возможных значения: 0 или 1. Комбинация битов позволяет представить любое число или символ.

Количество битов, необходимых для представления числа или символа, зависит от его диапазона значений. Например, для представления чисел от 0 до 3 достаточно 2 битов, а для представления чисел от 0 до 255 требуется 8 битов.

Двоичная система счисления удобна для использования в компьютерных системах, так как электронные коммутаторы в компьютерах имеют всего два состояния: включено (1) или выключено (0). Использование двоичной системы счисления позволяет упростить обработку информации и увеличить производительность компьютерных систем.

Для более удобного представления двоичных чисел используется система счисления с основанием 16, называемая шестнадцатеричной системой счисления. В шестнадцатеричной системе счисления цифры от 0 до 9 обозначаются числами от 0 до 9, а цифрами от 10 до 15 обозначаются буквы от A до F.

Десятичное число	Двоичное представление	Шестнадцатеричное представление
0000
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F

Двоичные числа и шестнадцатеричные числа широко используются в программировании и компьютерной науке. Знание двоичной системы счисления является фундаментальным для понимания работы компьютеров и программирования.

Преобразование чисел

Для преобразования двоичного числа в десятичное, каждая цифра двоичного числа умножается на 2 в степени, соответствующей ее позиции, и затем все полученные произведения суммируются. Например, двоичное число 1011 преобразуется в десятичное следующим образом:

1 * 23 + * 22 + 1 * 21 + 1 * 2 = 8 + 0 + 2 + 1 = 11

Для преобразования десятичного числа в двоичное, число делится последовательно на 2, пока не достигнет значения 0. Остатки от деления записываются в обратном порядке и образуют двоичное число. Например, десятичное число 14 преобразуется в двоичное следующим образом:

14 / 2 = 7 (остаток 0)

7 / 2 = 3 (остаток 1)

3 / 2 = 1 (остаток 1)

1 / 2 = (остаток 1)

Остатки 0, 1, 1, 1 записываются в обратном порядке, получается двоичное число 1110.

Также можно преобразовывать числа из десятичной системы счисления в другие системы, такие как восьмеричная и шестнадцатеричная, а также обратно.

Применение в компьютере

Системы счисления, такие как двоичная, восьмеричная и шестнадцатеричная, широко применяются в компьютере для представления и хранения информации. В основе работы компьютера лежит двоичная система счисления, где информация представлена в виде серии единиц (1) и нулей (0).

Каждый бит (бинарный разряд) может иметь два значения — 0 или 1. Комбинации битов могут представлять различные типы данных, такие как числа, символы и изображения. Например, в двоичной системе счисления число 1011 представляет собой комбинацию единиц и нулей, которая может быть интерпретирована как число 11 в десятичной системе.

Особенностью двоичной системы счисления является её простота и прямая связь с электронным оборудованием компьютера. Электрические сигналы в компьютере могут быть легко представлены двоичными цифрами, что делает их обработку и передачу внутри компьютерных систем более эффективными и надежными.

Для упрощения работы с большими числами и повышения эффективности хранения данных, иногда используются восьмеричная и шестнадцатеричная системы счисления. Восьмеричная система основана на числе 8 и использует цифры от 0 до 7, а шестнадцатеричная система использует цифры от 0 до 9 и буквы от A до F, чтобы представить числа от 0 до 15.

В компьютерных системах часто применяется шестнадцатеричная система, так как она позволяет компактно представлять большие числа и удобно работать с двоичными данными. Например, двоичное число 1101 может быть представлено как число D в шестнадцатеричной системе.

Использование различных систем счисления в компьютере помогает эффективно представлять и обрабатывать различные типы информации, такие как целые числа, числа с плавающей точкой, символы и цвета. Понимание этих систем счисления является неотъемлемой частью обучения программированию и компьютерным наукам.

4.13. Как представляются в компьютере вещественные числа?

Система вещественных чисел в математических вычислениях предполагается
непрерывной и бесконечной, т.е. не имеющей ограничений на диапазон и точность
представления чисел. Однако в компьютерах числа хранятся в регистрах и ячейках
памяти с ограниченным количеством разрядов. В следствие этого система
вещественных чисел, представимых в машине, является дискретной (прерывной)
и конечной.

При написании вещественных чисел в программах вместо привычной запятой
принято ставить точку. Для отображения вещественных чисел, которые могут быть как очень маленькими,
так и очень большими, используется форма записи чисел с порядком основания
системы счисления. Например, десятичное число 1.25 в этой форме можно представить так:

1.25 . 10 = 0.125 . 101 = 0.0125 . 102
= …
12.5 . 10-1 = 125.0 . 10-2 = 1250.0 . 10-3 = … .

Любое число N в системе счисления с основанием q можно записать в виде N = M . qp, где M множитель, содержащий все цифры числа (мантисса), а p целое число, называемое порядком. Такой способ записи чисел называется представлением числа с плавающей точкой.

Если «плавающая» точка расположена в мантиссе перед первой значащей цифрой,
то при фиксированном количестве разрядов, отведённых под мантиссу,
обеспечивается запись максимального количества значащих цифр числа, то есть
максимальная точность представления числа в машине. Из этого следует:

Мантисса должна быть правильной дробью, у которой первая цифра после точки (запятой в обычной записи) отлична от нуля: 0.12  M|  нормализованным

Мантиссу и порядок q-ичного числа принято записывать в системе с
основанием q, а само основание в десятичной системе.

Примеры нормализованного представления:
 
   Десятичная система        
                  Двоичная система

753.15 = 0.75315 . 103;     
       101.01 = 0.10101 . 211 (порядок 11₂ = 3₁₀)

0.000034 =  0.34 . 10-4;      
  0.000011 = 0.11 . 2-100 (порядок   100₂  =  4₁₀).

Вещественные числа в компьютерах различных типов записываются по-разному,
тем не менее, все компьютеры поддерживают несколько международных стандартных форматов,
различающихся по точности, но имеющих одинаковую структуру следующего вида:

Здесь порядок n-разрядного нормализованного числа задается в так
называемой смещенной форме: если для задания порядка выделено
k разрядов, то к истинному значению порядка, представленного
в дополнительном коде, прибавляют смещение, равное (2k-1  1).
Например, порядок, принимающий значения в диапазоне от 128 до +127,
представляется смещенным порядком, значения которого меняются от 0 до 255.

Использование смещенной формы позволяет производить операции над порядками,
как над беззнаковыми числами, что упрощает операции сравнения, сложения и
вычитания порядков, а также упрощает операцию сравнения самих нормализованных
чисел.

Чем больше разрядов отводится под запись мантиссы, тем выше точность
представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего
отличного от нуля числа до наибольшего числа, представимого в машине при
заданном формате.

Стандартные форматы представления вещественных чисел: 1) одинарный    32-разрядное нормализованное число со знаком, 8-разрядным смещенным порядком и 24-разрядной мантиссой (старший бит мантиссы, всегда равный 1, не хранится в памяти, и размер поля, выделенного для хранения мантиссы, составляет только 23 разряда). 2) двойной    64-разрядное нормализованное число со знаком, 11-разрядным смещенным порядком и 53-разрядной мантиссой (старший бит мантиссы не хранится, размер поля, выделенного для хранения мантиссы, составляет 52 разряда). 3) расширенный    80-разрядное число со знаком, 15-разрядным смещенным порядком и 64-разрядной мантиссой. Позволяет хранить ненормализованные числа.

Следует отметить, что вещественный формат с m-разрядной мантиссой
позволяет абсолютно точно представлять m-разрядные целые числа,
т. е. любое двоичное целое число, содержащее не более m разрядов,
может быть без искажений преобразовано в вещественный формат.

Единицы компьютерной информации

Выше уже было сказано, что бит — это минимально возможная единица информации, принимающая одно из двух взаимоисключающих значений: да/нет или 1/0. Однако сам по себе практической пользы бит не имеет, потому что его информационная емкость слишком мала, чтобы сохранить или передать хоть какие-то значимые данные. 

Блок из двух битов уже может принимать 4 возможных значения: 00, 01, 10, 11. Это уже позволяет закодировать некоторые числа, например 2 и 3. Совокупность трех битов дает уже 8 возможных значений. А блок из 8 битов позволяет составить 256 возможных комбинаций, чего вполне хватает для кодирования букв латинского алфавита со знаками препинания и спецсимволами. Благодаря данной практической ценности именно это количество битов стало считаться минимальной компьютерной единицей информации и получило название байт.

Но на практике кодировать приходится не просто отдельные буквы, а гораздо бо́льшие массивы данных: целые тексты, состоящие из тысяч и миллионов символов, аудио-, видеофайлы, изображения, программы и т. д. Для их хранения в двоичном коде необходимы тысячи, миллионы и миллиарды байтов. Чтобы упростить оперирование такими величинами, разработчики компьютерной техники стали оперировать более крупными обозначениями: 1 килобайт — 1024 байта, 1 мегабайт — 1024 килобайта, 1 гигабайт — 1024 мегабайта и т. д. 

Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.

Существуют позиционные и
непозиционные системы счисления.

В непозиционных
системах счисления
вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от
ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII
(тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах
счисления вес каждой
цифры изменяется в зависимости от ее положения (позиции) в последовательности
цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7
сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Сама же запись числа
757,7 означает сокращенную запись выражения:

Любая позиционная система
счисления характеризуется своим основанием.

Основание позиционной
системы счисления —
количество различных цифр, используемых для изображения чисел в данной системе
счисления.

За основание системы
можно принять любое натуральное число — два, три, четыре и т.д. Следовательно,
возможно бесчисленное множество позиционных систем: двоичная, троичная,
четверичная и т.д.

Основные позиционные СС, правила перевода

Двоичная система счисления

Систему, на которой основывается работа компьютеров, придумал гениальный немецкий ученый Г.В. Лейбниц (еще до 19 века!). Он придумал и описал СС, в которой все вычисления проводятся при помощи двух простейших символов – 0 и 1.

Компьютер, как механическое устройство, получает команды в виде двоичной кодировки. Он не в силах понять сложные задания, человеческую речь, музыку или тысячи оттенков, а переводя/кодируя всю необходимую информацию при помощи 0 и 1 (сеть, отсутствие сети), можно передать ему любые команды или информацию. Естественно, такие задания выглядят как огромные массивы двух знаков.

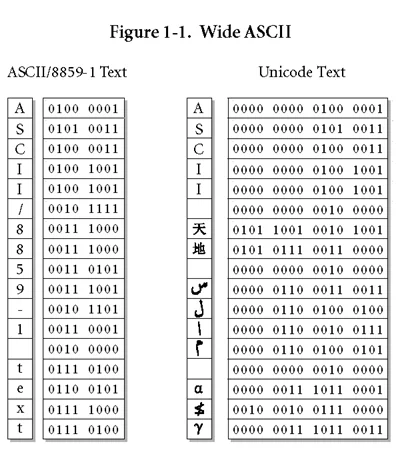
Алгоритм перевода чисел из десятичной в двоичную систему:

1. Деление на основу СС до тех пор, пока не останется в остатке значение меньше значения основы.
2. Записать остатки, от последнего к первому.
3. Первый ноль можно не писать.

111 0100 1100₂ 

Этот порядок действия позволят переводить в любую позиционную СС. В данном случае, основа – 2, остаток < или равен =.

Обратный алгоритм перевода из двоичной в десятичную систему счисления:

Записать число развернуто, то есть, сколько сотен, десятков и единиц в нем, но учитывая основу – 2

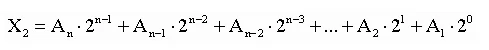
Объяснение. Развернутая форма записи 579: 5*102+7*101+9*10= 579₁₀.

Обычно мы пользуемся свернутой формой записи чисел, то есть без разбивки на разряды и умножения на основу.

1. Умножить и суммировать полученные значения.

А чтобы было легче, пользуются готовой таблицей степеней 2.

Альтернативный способ преобразования для гуманитариев

Для начала нужно написать степени двойки, начиная с самой большой:

Далее нужно отнимать от числа максимальную степень двойки и напротив нее ставить 1, если есть в исходном варианте или 0, если его нет. Перевод числа 579

Обратно еще проще. Подсчитать количество знаков – это будет степень 2 в степени -1. И так далее. А проще при помощи той же таблицы:

Если же оно на 1 больше, то число будет начинаться и заканчиваться на 1, а внутри – сплошные 0.

Восьмеричная СС

Основой такой системы является 8, а числа восьмеричной системы 0-7. Данная система счисления является позиционной и целочисленной. Применяется в сферах, связанных с цифровыми технологиями, особенно в Linux-программном обеспечении (права доступа, исполнения).

Пример: Перевести 579₈ из десятичной в восьмеричную систему счисления:

Обратный перевод из восьмеричной СС в десятичную:

1103₈ = 1∙83+1∙82+0∙81+3∙8 = 512+64+0+3 = 579₁₀

Таблица степеней

Альтернативный вариант таблицы степеней